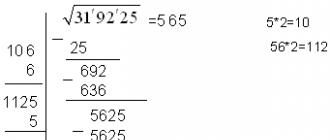Квадратный корень по методу евклида. Нахождение НОД по алгоритму Евклида и с помощью разложения на простые множители. Целые положительные числа

В предисловии к своему первому изданию “В царстве смекалки” (1908 год) Е. И. Игнатьев пишет: “... умственную самодеятельность, сообразительность и “смекалку” нельзя ни “вдолбить”, ни “вложить” ни в чью голову. Результаты надёжны лишь тогда, когда введение в область математических знаний совершается в лёгкой и приятной форме, на предметах и примерах обыденной и повседневной обстановки, подобранных с надлежащим остроумием и занимательностью”.

В предисловии к изданию 1911 г “Роль памяти в математике” Е.И. Игнатьев пишет “… в математике следует помнить не формулы, а процесс мышления”.

Для извлечения квадратного корня существуют таблицы квадратов для двухзначных чисел, можно разложить число на простые множители и извлечь квадратный корень из произведения. Таблицы квадратов бывает недостаточно, извлечение корня разложением на множители - трудоёмкая задача, которая тоже не всегда приводит к желаемому результату. Попробуйте извлечь квадратный корень из числа 209764? Разложение на простые множители дает произведение 2*2*52441. Методом проб и ошибок, подбором – это, конечно, можно сделать, если быть уверенным в том, что это целое число. Способ, который я хочу предложить, позволяет извлечь квадратный корень в любом случае.

Когда-то в институте (Пермский государственный педагогический институт) нас познакомили с этим способом, о котором сейчас хочу рассказать. Никогда не задумывалась, есть ли у этого способа доказательство, поэтому сейчас пришлось некоторые доказательства выводить самой.

Основой этого способа, является состав числа =.

=&, т.е. & 2 =596334.

1. Разбиваем число (5963364) на пары справа налево (5`96`33`64)

2. Извлекаем квадратный корень из первой слева группы ( - число 2). Так мы получаем первую цифру числа &.

3. Находим квадрат первой цифры (2 2 =4).

4. Находим разность первой группы и квадрата первой цифры (5-4=1).

5.Сносим следующие две цифры (получили число 196).

6. Удваиваем первую, найденную нами цифру, записываем слева за чертой (2*2=4).

7.Теперь необходимо найти вторую цифру числа &: удвоенная первая цифра, найденная нами, становится цифрой десятков числа, при умножении которого на число единиц, необходимо получить число меньшее 196 (это цифра 4, 44*4=176). 4 - вторая цифра числа &.

8. Находим разность (196-176=20).

9. Сносим следующую группу (получаем число 2033).

10. Удваиваем число 24, получаем 48.

11.48 десятков в числе, при умножении которого на число единиц, мы должны получить число меньшее 2033 (484*4=1936). Найденная нами цифра единиц (4) и есть третья цифра числа &.

Доказательство приведено мной для случаев:

1. Извлечение квадратного корня из трехзначного числа;

2. Извлечение квадратного корня из четырехзначного числа.

Приближенные методы извлечения квадратного корня (без использования калькулятора) .

1.Древние вавилоняне пользовались следующим способом нахождения приближенного значения квадратного корня их числа х. Число х они представляли в виде суммы а 2 +b, где а 2 ближайший к числу х точный квадрат натурального числа а (а 2 ?х), и пользовались формулой . (1)

Извлечем с помощью формулы (1) корень квадратный, например из числа 28:

Результат извлечения корня из 28 с помощью МК 5,2915026.

Как видим способ вавилонян дает хорошее приближение к точному значению корня.

2. Исаак Ньютон разработал метод извлечения квадратного корня, который восходил еще к Герону Александрийскому (около 100 г. н.э.). Метод этот (известный как метод Ньютона) заключается в следующем.

Пусть а 1 - первое приближение числа (в качестве а 1 можно брать значения квадратного корня из натурального числа - точного квадрата, не превосходящего х) .

Следующее, более точное приближение а 2 числа найдется по формуле .

Рассмотрим этот алгоритм на примере. Найдем

1-й шаг. Число под корнем разбиваем на грани по две цифры (справа налево):

2-й шаг. Извлекаем квадратный корень из первой грани, т. е. из числа 65, получаем число 8. Под первой гранью пишем квадрат числа 8 и вычитаем. К остатку приписываем вторую грань (59):

(число 159 - первый остаток).

3-й шаг. Удваиваем найденный корень и пишем результат слева:

4-й шаг. Отделяем в остатке (159) одну цифру справа, слева получаем число десятков (оно равно 15). Затем делим 15 на удвоенную первую цифру корня, т. е. на 16, так как 15 на 16 не делится, то в частном получается нуль, который записываем как вторую цифру корня. Итак, в частном получили число 80, которое опять удваиваем, и сносим следующую грань

(число 15 901 - второй остаток).

5-й шаг. Отделяем во втором остатке одну цифру справа и полученное число 1590 делим на 160. Результат (цифру 9) записываем как третью цифру корня и приписываем к числу 160. Полученное число 1609 умножаем на 9 и находим следующий остаток (1420):

В дальнейшем действия выполняются в той последовательности, которая указана в алгоритме (корень можно извлекать с нужной степенью точности).

Замечание. Если подкоренное выражение - десятичная - дробь, то ее целую часть разбивают на грани по две цифры справа налево, дробную часть - по две цифры слева направо и извлекают корень по указанному алгоритму.

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

1. Извлеките квадратный корень из числа: а) 32; б) 32,45; в) 249,5; г) 0,9511.

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.

Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.

Алгоритм нахождения НОД делением

1. Большее число делим на меньшее.
2. Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
3. Если есть остаток, то большее число заменяем на остаток от деления.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 / 18 = 1 (остаток 12)
18 / 12 = 1 (остаток 6)
12 / 6 = 2 (остаток 0)
Конец: НОД – это делитель 6.
НОД (30, 18) = 6

a = 50 b = 130 while a != 0 and b != 0 : if a > b: a = a % b else : b = b % a print (a + b)

В цикле в переменную a или b записывается остаток от деления. Цикл завершается, когда хотя бы одна из переменных равна нулю. Это значит, что другая содержит НОД. Однако какая именно, мы не знаем. Поэтому для НОД находим сумму этих переменных. Поскольку в одной из переменных ноль, он не оказывает влияние на результат.

Алгоритм нахождения НОД вычитанием

1. Из большего числа вычитаем меньшее.
2. Если получается 0, то значит, что числа равны друг другу и являются НОД (следует выйти из цикла).
3. Если результат вычитания не равен 0, то большее число заменяем на результат вычитания.
4. Переходим к пункту 1.

Пример:
Найти НОД для 30 и 18.
30 - 18 = 12
18 - 12 = 6
12 - 6 = 6
6 - 6 = 0
Конец: НОД – это уменьшаемое или вычитаемое.
НОД (30, 18) = 6

a = 50 b = 130 while a != b: if a > b: a = a - b else : b = b - a print (a)

Эта статья про нахождение наибольшего общего делителя (НОД) двух и большего количества чисел. Сначала рассмотрим алгоритм Евклида, он позволяет находить НОД двух чисел. После этого остановимся на методе, позволяющем вычислять НОД чисел как произведение их общих простых множителей. Дальше разберемся с нахождением наибольшего общего делителя трех и большего количества чисел, а также приведем примеры вычисления НОД отрицательных чисел.

Навигация по странице.

Алгоритм Евклида для нахождения НОД

Заметим, что если бы мы с самого начала обратились к таблице простых чисел , то выяснили бы, что числа 661 и 113 – простые, откуда можно было бы сразу сказать, что их наибольший общий делитель равен 1 .

Ответ:

НОД(661, 113)=1 .

Нахождение НОД с помощью разложения чисел на простые множители

Рассмотрим еще один способ нахождения НОД. Наибольший общий делитель может быть найден по разложениям чисел на простые множители . Сформулируем правило: НОД двух целых положительных чисел a и b равен произведению всех общих простых множителей, находящихся в разложениях чисел a и b на простые множители .

Приведем пример для пояснения правила нахождения НОД. Пусть нам известны разложения чисел 220 и 600 на простые множители, они имеют вид 220=2·2·5·11 и 600=2·2·2·3·5·5 . Общими простыми множителями, участвующими в разложении чисел 220 и 600 , являются 2 , 2 и 5 . Следовательно, НОД(220, 600)=2·2·5=20 .

Таким образом, если разложить числа a и b на простые множители и найти произведение всех их общих множителей, то этим будет найден наибольший общий делитель чисел a и b .

Рассмотрим пример нахождения НОД по озвученному правилу.

Пример.

Найдите наибольший общий делитель чисел 72 и 96 .

Решение.

Разложим на простые множители числа 72 и 96 :

То есть, 72=2·2·2·3·3 и 96=2·2·2·2·2·3 . Общими простыми множителями являются 2 , 2 , 2 и 3 . Таким образом, НОД(72, 96)=2·2·2·3=24 .

Ответ:

НОД(72, 96)=24 .

В заключение этого пункта заметим, что справедливость приведенного правила нахождения НОД следует из свойства наибольшего общего делителя, которое утверждает, что НОД(m·a 1 , m·b 1)=m·НОД(a 1 , b 1) , где m – любое целое положительное число.

Нахождение НОД трех и большего количества чисел

Нахождение наибольшего общего делителя трех и большего количества чисел может быть сведено к последовательному нахождению НОД двух чисел. Мы об этом упоминали, при изучении свойств НОД. Там мы сформулировали и доказали теорему: наибольший общий делитель нескольких чисел a 1 , a 2 , …, a k равен числу d k , которое находится при последовательном вычислении НОД(a 1 , a 2)=d 2 , НОД(d 2 , a 3)=d 3 , НОД(d 3 , a 4)=d 4 , …, НОД(d k-1 , a k)=d k .

Давайте разберемся, как выглядит процесс нахождения НОД нескольких чисел, рассмотрев решение примера.

Пример.

Найдите наибольший общий делитель четырех чисел 78 , 294 , 570 и 36 .

Решение.

В этом примере a 1 =78 , a 2 =294 , a 3 =570 , a 4 =36 .

Сначала по алгоритму Евклида определим наибольший общий делитель d 2 двух первых чисел 78 и 294 . При делении получаем равенства 294=78·3+60 ; 78=60·1+18 ; 60=18·3+6 и 18=6·3 . Таким образом, d 2 =НОД(78, 294)=6 .

Теперь вычислим d 3 =НОД(d 2 , a 3)=НОД(6, 570) . Опять применим алгоритм Евклида: 570=6·95 , следовательно, d 3 =НОД(6, 570)=6 .

Осталось вычислить d 4 =НОД(d 3 , a 4)=НОД(6, 36) . Так как 36 делится на 6 , то d 4 =НОД(6, 36)=6 .

Таким образом, наибольший общий делитель четырех данных чисел равен d 4 =6 , то есть, НОД(78, 294, 570, 36)=6 .

Ответ:

НОД(78, 294, 570, 36)=6 .

Разложение чисел на простые множители также позволяет вычислять НОД трех и большего количества чисел. В этом случае наибольший общий делитель находится как произведение всех общих простых множителей данных чисел.

Пример.

Вычислите НОД чисел из предыдущего примера, используя их разложения на простые множители.

Решение.

Разложим числа 78 , 294 , 570 и 36 на простые множители, получаем 78=2·3·13 , 294=2·3·7·7 , 570=2·3·5·19 , 36=2·2·3·3 . Общими простыми множителями всех данных четырех чисел являются числа 2 и 3 . Следовательно, НОД(78, 294, 570, 36)=2·3=6 .

Размер: px

Начинать показ со страницы:

Транскрипт

1 ЛЕКЦИЯ 2 ВЫЧИСЛЕНИЕ НАИБОЛЬШЕГО ОБЩЕГО ДЕЛИТЕЛЯ Алгоритм Евклида При работе с большими составными числами их разложение на простые множители, как правило, неизвестно. Но для многих прикладных задач теории чисел поиск разложения числа на множители является важной, часто встречающейся практической задачей. В теории чисел существует сравнительно быстрый способ вычисления НОД двух чисел, который называется алгоритмом Евклида. Алгоритм 1. Алгоритм Евклида . Вход. Целые числа а, b; 0 < b < а. Выход. d = НОД (a,b). 1. Положить r 0 a, r 1 b, i Найти остаток r i+1 от деления r i 1 на r i. 3. Если r i+1 = 0, то положить d r i. В противном случае положить i i + 1 и вернуться на шаг Результат: d. Теорема. Для любых а, b > 0 алгоритм Евклида останавливается и выдаваемое им число d является наибольшим общим делителем чисел а и b. Доказательство . По теореме о делении с остатком для любого i 1 имеем r i 1 = q i r i + r i+1, где 0 r i+1 < r i. Получаем монотонно убывающую последовательность неотрицательных целых чисел r 1 > r 2 > r 3 >... 0, ограниченную снизу. Такая последовательность не может быть бесконечной, следовательно, алгоритм Евклида останавливается. Бинарный алгоритм Евклида Бинарный алгоритм Евклида вычисления НОД оказывается более быстрым при реализации этого

2 алгоритма на компьютере, поскольку использует двоичное представление чисел а и b. Бинарный алгоритм Евклида основан на следующих свойствах наибольшего общего делителя (считаем, что 0 < b а): 1) если оба числа а и b четные, то НОД(a,b) = 2 НОД(a/2, b/2) 2) если число а нечетное, число b четное, то НОД(a, b) = НОД(а, b/2); 3) если оба числа а и b нечетные, а > b, то НОД(а, b) = НОД(а b, b); 4) если а = b, то НОД(а, b) = а. Алгоритм 2. Бинарный алгоритм Евклида . Вход. Целые числа a, b; 0 < b а. Выход. d = HOД(a,b). 1. Положить g Пока оба числа а и b четные, выполнять а a/2, b b/2, g 2g до получения хотя бы одного нечетного значения а или b. 3. Положить u a, v b. 4. Пока u 0, выполнять следующие действия Пока u четное, полагать u u/ Пока v четное, полагать v v/ При u v положить u u v. В противном случае положить v v u. 5. Положить d gv. 6. Результат: d. Расширенный алгоритм Евклида Расширенный алгоритм Евклида находит наибольший общий делитель d чисел а и b и его линейное представление, т. е. целые числа x и у, для которых ах + by = d, и не требует «возврата», как в рассмотренном примере. Пусть d НОД для a и b, т. е. d = (a, b), где a > b. Тогда существуют такие целые числа x и y, что d = ax + by. Иными словам, НОД двух чисел можно представить в

3 виде линейной комбинации этих чисел с целыми коэффициентами. Алгоритм 3. Схема расширенного алгоритма Евклида. 1. Определить = 1, = 0, = 0, = 1, α = a, β = b. 2. Пусть число q частное от деления числа a на число b, а число r остаток от деления этих чисел (т. е. a = qb + r). a = b; b = r; t = ; //t = x i-1 ; = t q; // = x i для правой части = x i+1 для правой; //t = y i-1 ; = t q; 5. Возвращаемся на шаг Определяем x = x 0, y = y 0, d = αx + βy. Вариант расширенного алгоритма Евклида Вход. Целые числа а, b; 0 < b а. Выход: d = НОД(а, b); такие целые числа х, у, что ах + by = d. 1. Положить r 0 а, r 1 b, х 0 1, x 1 0, у 0 0, y 1 1, i 1 2. Разделить с остатком r i 1 на r i,: r i 1 = q i r i +r i Если r i+1 = 0, то положить d r i, х x i у y i. В противном случае положить x i+1 x i 1 x i, y i+1 y i 1 y i, i i + 1 и вернуться на шаг Результат: d, х, у. Корректность определения чисел х и у,

4 вычисляемых алгоритмом, показывает следующая теорема. Теорема 4. На каждой итерации алгоритма 3 выполняется равенство аx i + by i = r i, при i 0. Доказательство . Воспользуемся методом математической индукции. Для i = 0 и i = 1 требуемое равенство имеет место в силу шага 1 алгоритма 3. Допустим, что оно справедливо для i 1 и для i. Тогда на шаге 3 получаем x i+1 = x i 1 x i и y i+1 = y i 1 y i. Следовательно, аx i+1 + by i+1 = a(x i 1 x i) + b(y i 1 y i,) = ax i 1 + by i 1 (ax i + by i) = r i 1 r i = r i+1. Пример. Дано a = 1769, b = 551. Используя расширенный алгоритм Эвклида, найти целые числа x и y такие, что d = ax + by, где d НОД чисел a и b. I этап последовательности вычислений. 1. Определить = 1, = 0, = 0, = 1, α = 1769, β = Частное от деления q = a/b = 1769/551 = 3, а остаток от деления r = 116. a = 551; b = 116; t = =0: = t q = 1 0 = 1 = 0; = t q = 3; следующие промежуточные значения

5 параметров: a= 551, b = 116, = 0, = 1, = 1, = Так как остаток от деления r 0, то возвращаемся на шаг 2. II этап последовательности вычислений. 1. Значение параметров: a = 551, b = 116, = 0, = 1, = 1, = Частное от деления q = a/b = 551/116 = 4, а остаток от деления r = 87. a = 116; b = 87; t = = 0; =1: = t q = = 4 = 3; = t q = 1 (3) 4 = 13; следующие промежуточные значения параметров: a= 116, b = 87, = 1, = 4, = 3, = Так как остаток от деления r 0, то возвращаемся на шаг 2. III этап последовательности вычислений. 1. Значение параметров: a= 116, b = 87, = 1, = 4, = 3, = Частное от деления q = a/b = 116/87 = 1, а остаток от деления r = 29.

6 a = 87; b = 29; t = = 4: = t q = 1 (4) 1 = 5; = 3; = 13; = t q = 3 (13) 1 = 16; следующие промежуточные значения параметров: a= 87, b = 29, = 4, = 5, = 13, = Так как остаток от деления r 0, то возвращаемся на шаг 2. IV этап последовательности вычислений. 1. Значение параметров: a= 87, b = 29, = 4, = 5, = 13, = Частное от деления q = a/b = 87/29 = 3, а остаток от деления r = 0. a = 87; b = 29; t = = 4; = 5; = 19; = 13; = 16; = t q = 13 (16) 3 = 61; следующие промежуточные значения параметров: a= 87, b = 29, = 5, = 19, = 16, = Так как остаток от деления r = 0, то выполняем шаг 6.

7 6. Вычисляем НОД по формуле d = αx + βy, где x = x 0 = 5, y = y 0 = 16, α= 1769, β = 551. Подставляя значение параметров, получаем d = αx + βy = = = 29. Расширенный алгоритм Евклида можно реализовать и в двоичном виде. Алгоритм 4. Расширенный бинарный алгоритм Евклида . Вход. Целые числа а, b; 0 < b а. Выход. d = НОД(a, b); такие целые числа х, у, что ах + by = d. 1. Положить g Пока оба числа а и b четные, выполнять а a/2, b b/2, g 2g до получения хотя бы одного нечетного значения а или b. 3. Положить u a, v b, А 1, В 0, С 0, D Пока u 0, выполнять следующие действия Пока u четное, положить u u/ Если оба числа А и B четные, то положить A A/2, B B/2. В противном случае положить A (A+b)/2, B (B a)/ Пока v четное: Положить v v/ Если оба числа С и D четные, то положить С C/2, D D/2. В противном случае положить C (C + b)/2, D (D a)/ При u v положить u u v, А А С, В В D. В противном случае положить v v u, C C A, D D B. 5. Положить d gv, x С, у D. 6. Результат: d, х, у.

Решение уравнений в целых числах Линейные уравнения. Метод прямого перебора Пример. В клетке сидят кролики и фазаны. Всего у них 8 ног. Узнать сколько в клетке тех и других. Укажите все решения. Решение.

Занятие 7 Число d называется наибольшим общим делителем (НОД) чисел a и b, если (1) d a и d b, а также (2) для всех x из x a и x b следует x d. В этом случае пишем d = (a, b). Лемма 1. Для любых чисел

Тема. Основы элементарной теории чисел и приложения- Теоретический материал. Множество вычетов по модулю, свойства сравнений. Пусть натуральное число, большее. Через Z обозначаем множество всех классов

Югорский физико-математический лицей ВП Чуваков ОСНОВЫ ТЕОРИИ ЧИСЕЛ Конспект лекций (0)(mod) (0)(mod) Натуральные числа N, - множество натуральных чисел, используемых для счета или перечисления

Глава 2 Целые, рациональные и вещественные числа 2.. Целые числа Числа, 2, 3,... называются натуральными. Множество всех натуральных чисел обозначается N, т.е. N = {,2,3,...}. Числа..., 3, 2,0,2,3,...

Цепные дроби Конечные цепные дроби Определение Выражение вида a 0 + a + a + + a m где a 0 Z a a m N a m N/{} называется цепной дробью а m - длиной цепной дроби a 0 a a m будем называть коэффициентами цепной

ЛЕКЦИЯ 1 НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ В пособии не излагается теория чисел а дан минимальный инструментарий из этой теории который в дальнейшем потребуется для изучения криптографических систем используемых

Горбачев НЕ Многочлены от одной переменной Решение уравнений степени Понятие многочлена Арифметические операции над многочленами Опр Многочленом (полиномом) -й степени относительно переменной величины

Делимость целых чисел Число а делится на число b (или b делит а) если существует такое число с, что а=bc При этом число c называется частным от деления а на b Обозначения: a - а делится на b или ba b делит

ЛЕКЦИЯ 12 СРВНЕНИЯ ВТОРОЙ СТЕПЕНИ ПО ПРОСТОМУ МОДУЛЮ И КВАДРАТИЧНЫЕ ВЫЧЕТЫ Общий вид сравнения второй степени по простому модулю р имеет вид (1) с 0 х 2 + с 1 х + с 2 0 mod p. Поиск решения сравнения (1)

Указания, решения, ответы УРАВНЕНИЯ В ЦЕЛЫХ ЧИСЛАХ. Уравнение с одной неизвестной.. Решение. Подставим в уравнение. Получим равенство (4a b 4) (a b 8) 0. Равенство A B 0, где А и В целые, выполняется,

Алгебраические многочлены. 1 Алгебраические многочлены степени n над полем K Определение 1.1 Многочленом степени n, n N {0}, от переменной z над числовым полем K называется выражение вида: fz = a n z n

Лекция Квадратичные вычеты и невычеты Лектор: НЮ Золотых Записал: Е Замараева?? сентября 00 Содержание Квадратичные вычеты и невычеты Символ Лежандра Свойства символа Лежандра Квадратичный закон взаимности

ГОУ Школа-интернат ""Интеллектуал"" И с с л е д о в а т е л ь с к а я р а б о т а п о м а т е м а т и к е на тему: «О представимости натуральных чисел в виде линейной комбинации с целыми коэффициентами»

Математический анализ Раздел: Неопределенный интеграл Тема: Интегрирование рациональных дробей Лектор Пахомова Е.Г. 0 г. 5. Интегрирование рациональных дробей ОПРЕДЕЛЕНИЕ. Рациональной дробью называется

4 Теория чисел 4 Целые числа 7 Определение Пусть, b Z Тогда делит b, если существует целое число такое что b (обозначается b) 73 Теорема (деление с остатком) Если, b Z и b, тогда найдутся такие целые

Математический анализ Раздел: Неопределенный интеграл Тема: Интегрирование рациональных дробей Лектор Рожкова С.В. 0 г. 5. Интегрирование рациональных дробей ОПРЕДЕЛЕНИЕ. Рациональной дробью называется

009-00 уч. год. 6, 9 кл. Математика. Элементы теории чисел. 4. Вычисление наибольшего общего делителя и наименьшего общего кратного Сохраним обозначения из параграфа. Для натурального числа n запись n

ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). I 1 / 67 Часть I Конечные поля (поля Галуа). I ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа). I 2 / 67 Поля вычетов по модулю простого

5 Решение уравнений в целых числах В решении даже таких простейших уравнений, как линейное уравнение с одним неизвестным, есть свои особенности, если коэффициенты уравнения являются целыми числами, и требуется

Лабораторная работа 8 Вычисление наибольшего общего делителя для двух чисел при помощи алгоритма Евклида Цель работы используя алгоритм Эвклида создать программу, которая для чисел a и b определяет наибольший

Раздел 1. Математические основы криптографии 1 Определение поля Конечным полем GF q (или полем Галуа) называют конечное произвольное множество элементов с заданными между ними операциями сложения, умножения

XIX Межрегиональная олимпиада школьников по математике и криптографии Задачи для 11 класса Решение задачи 1 Сначала заметим, что если N = pq, где p и q простые числа, то количество натуральных чисел, меньших

Многочлены и их корни 2018 г. Гущина Елена Николаевна Определение: Многочленом степени n n N называется всякое выражение вида: P & z = a & z & + a &+, z &+, + + a, z + a., где a &, a &+, a, a. R, a &

Лекция 4. СТАНДАРТ AES. АЛГОРИТМ RIJNDAEL. Стандарт AES (Advnced Encrypton Stndrd) представляет собой новый стандарт шифрования с одним ключом, который заменил стандарт DES. Алгоритм Rjndel (рейн-дал)

Многочлены и их корни Определение: Многочленом степени n (n N) называется всякое выражение вида: P n (z) = a n z n + a n 1 z n 1 + + a 1 z + a 0, где a n, a n 1, a 1, a 0 R, a n старший коэффициент, a

1 Алгоритм Евклида и его сложность Определение 1. Общим делителем чисел a и b называется такое число c, что c a и c b. Определение 2. Наибольшим общим делителем чисел a и b называется такой их общий делитель,

ЛЕКЦИЯ 14 Вычисление квадратных корней по составному модулю Из приведенной выше теории следует, что если =, где и простые числа, группа Z изоморфна пространству Z Z. Поскольку изоморфизм сохраняет свойства

ЛЕКЦИЯ 3 ВЫЧИСЛЕНИЕ КВАДРАТНЫХ КОРНЕЙ ПО МОДУЛЮ Случай простого модуля Рассмотрим сравнение х a mod р, () где число р простое и целое число а не делится на p Вычисление решения x данного уравнения является

Программа коллоквиума по дискретной математике (основной поток) В начале коллоквиума Вы получите билет, в котором будет три вопроса: вопрос на знание определений, задача, вопрос на знание доказательств.

Алгоритм Шора Ю. Лифшиц. 1 декабря 005 г. План лекции 1. Подготовка (a) Разложение чисел на множители (b) Квантовые вычисления (c) Эмуляция классических вычислений. Алгоритм Саймона (a) Квантовый параллелизм

Из истории математики Первой достаточно объемной книгой, в которой арифметика излагалась независимо от геометрии, было Введение в арифметику Никомаха (ок нэ) В истории арифметики её роль сравнима с ролью

Краткое введение в начала элементарной теории чисел Денис Кириенко Летняя компьютерная школа, 1 января 2009 года Целочисленное деление Пусть дано два целых числа a и b, b 0. Целочисленным частным от деления

Тема 1-9: Многочлены. Построение кольца многочленов. Теория делимости. Производная А. Я. Овсянников Уральский федеральный университет Институт математики и компьютерных наук кафедра алгебры и дискретной

Алгебраические уравнения где Определение. Алгебраическим называется уравнение вида 0, P () 0, некоторые действительные числа. 0 0 При этом переменная величина называется неизвестным, а числа 0, коэффициентами

Лекция 6 Элементы теории чисел 1 Задача. Продолжите числовой ряд 1, 3, 5, 7, 1, 3, 5, 7, 11 1, 11, 101, 1001, 1, 11, 101, 1001, 1011, 2 Арифметика целых чисел Использует целые числа: Z = {, -2, -1, 0,

Многочлены Многочленом с одной переменной х степени n называют выражение вида, где - любые числа, называемые коэффициентами многочлена, причем называют старшим коэффициентом многочлена Если вместо переменной

1 2 Содержание. 1. Введение. 4-6 1.1. Аннотация...4 1.2. Проблема 4 1.3. Цель работы 5 1.4. Гипотеза..5 1.5. Предмет исследования... 5 1.6. Объект исследования. 5 1.7. Новизна... 5-6 1.8. Методы исследования...6

8.3, 8.4.2 класс, Математика (учебник Макарычев) 2018-2019 уч.год Тема модуля «Целые числа. Делимость чисел. Степень с целым показателем» В тесте проверяются теоретическая и практическая части. ТЕМА Знать

Лекция ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ Рациональные дроби Интегрирование простейших рациональных дробей Разложение рациональной дроби на простейшие дроби Интегрирование рациональных дробей Рациональные

Www.cryptolymp.ru XIX Межрегиональная олимпиада школьников по математике и криптографии (11 класс) Решение задачи 1 Сначала заметим, что если N pq, где p и q простые числа, то количество натуральных чисел,

Глава Целые числа Теория делимости Целыми называются числа, -3, -, -, 0, 3, те натуральные числа, 3, 4, а также нуль и отрицательные числа -, -, -3, -4, Множество всех целых чисел обозначается через

Министерство образования и науки РФ Уральский государственный экономический университет Ю. Б. Мельников Многочлены Раздел электронного учебника для сопровождения лекции Изд. 4-е, испр. и доп. e-mail: [email protected],

{тригонометрический ряд тригонометрическая система примеры - разложение на интервале [ -l; l ] для функций произвольного периода - неполные ряды разложение по синусам и косинусам четные и нечетные продолжения}

Теоретическая информатика II Лекция 5. Целочисленные алгоритмы: расширенный алгоритм Евклида, обратный элемент по модулю, возведение в степень по модулю. Криптография с открытым ключом, протокол RSA. Вероятностная

5. Коды Боуза-Чоудхури-Хоквингема Корректирующие свойства циклических кодов могут быть определены на основе двух теорем . Теорема 1. Для любых m и t существует циклический код длиной n = 2 m 1, с кратностью

МОДУЛЬНАЯ АРИФМЕТИКА В некоторых приложениях удобно выполнять арифметические операции над целыми числами, заданными в так называемом модульном представлении Это представление предполагает, что целое число

МАТЕМАТИКА ЕГЭ 00 Корянов А.Г. Задания С г. Брянск Замечания и пожелания направляйте по адресу: [email protected] УРАВНЕНИЯ И НЕРАВЕНСТВА В ЦЕЛЫХ ЧИСЛАХ (от учебных задач до олимпиадных задач) Линейные

2.22. Вынесите за скобки общий множитель (n натуральное число): 1) x n + 3 + x n ; 3) z 3n - z n ; 2) y n + 2 - y n - 2, n > 2; 4) 5 n + 4 + 2 5 n + 2-3 5 n + 1. 2.23. Каждому числу поставили в соответствие

ЛЕКЦИЯ 15 ПРОСТЫЕ ЧИСЛА Натуральное число p, больше единицы называется простым, если оно делится нацело только на 1 и на себя. Теорема (Эвклид). Множество простых чисел бесконечно. Обозначим через π(x)

Тема 3. Элементы алгебраической и аналитической теории чисел Теоретический материал 1. Цепные дроби. Конечной цепной дробью называется выражение a +, (1) где a - целое число, a, i > 0, натуральные числа,

Http://vk.ucoz.et/ Операции над многочленами k a k Многочленом (полиномом) степени k называется функция вида a, где переменная, a - числовые коэффициенты (=,.k), и. Любое ненулевое число можно рассматривать

Пензенский государственный педагогический университет имени В. Г. Белинского М. В. Глебова В. Ф. Тимербулатова ПРАКТИЧЕСКИЕ ЗАНЯТИЯ ПО АЛГЕБРЕ МНОГОЧЛЕНОВ Учебно-методическое пособие Пенза Печатается по

ДЕЛИМОСТЬ ЦЕЛЫХ ЧИСЕЛ С ОСТАТКОМ Пусть m целое число, а n натуральное число Если m > n и m не делится на n нацело, то возможно деление m на n с остатком Определение 3 Для любого целого числа m и любого

Авдошин С.М., Савельева А.А. Алгоритм решения систем линейных уравнений в кольцах вычетов Разработан эффективный алгоритм решения систем линейных уравнений в кольцах вычетов , эквивалентный по сложности

ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа) I 1 / 88 Часть I Конечные поля (поля Галуа) I ПРИКЛАДНАЯ АЛГЕБРА. Часть I: Конечные поля (поля Галуа) I 2 / 88 Поля вычетов по модулю простого числа

5 Алгебраические структуры 6 Определение Бинарная операция на множестве S есть отображение S S в S То есть, является правилом, которое каждой упорядоченной паре элементов из S ставит в соответствие некоторый

/Е Э лементы теории чисел и. рочев 28 августа 2018 г. Оглавление Оглавление i 1 Целые числа 1 1.1 Вводные задачи....................................... 1 1.2 Наибольший общий делитель..............................

Глава Целые, рациональные и действительные числа. Деление с остатком. Каждое из чисел ±23, ±4 разделите с остатком на каждое из чисел ±5. 2. Найдите все положительные делители числа 42. 3. Сейчас 3 часов.

Дифференциальные уравнения лекция 4 Уравнения в полных дифференциалах. Интегрирующий множитель Лектор Шерстнёва Анна Игоревна 9. Уравнения в полных дифференциалах Уравнение d + d = 14 называется уравнением

Тема. Основы элементарной теории чисел и приложения-. Первообразные корни, индексы. Теоретический материал Пусть а, m натуральные взаимно простые числа, причем m, тогда, согласно теореме Эйлера, a m)

Кафедра математики и информатики Элементы высшей математики Учебно-методический комплекс для студентов СПО, обучающихся с применением дистанционных технологий Модуль Теория пределов Составитель: доцент

Раздел 2. Теоретико-численные методы в криптографии Задание на самостоятельную работу Изучить алгоритмы, которые широко применяются в криптографии. Элементы теории чисел: расширенный алгоритм Евклида;

Тематический план составлен на основе программного материала 206-207 уч.года по учебнику «Алгебра 8» под ред. А.Г.Мордковича с учетом рекомендованного обязательного минимума содержания образования Тема

Лекция 2. Свойства биномиальных коэффициентов. Подсчет сумм и метод производящих функций (конечный случай). Полиномиальные коэффициенты. Оценки биномиальных и полиномиальных коэффициентов. Оценки сумм