Opštinski budžet obrazovne ustanove

Srednja škola Doschatinskaya

gradski okrug Vyksa, oblast Nižnji Novgorod

Rješavanje logičkih problema.

Odsjek za fiziku i matematiku

Sekcija matematika

Uradio sam posao:

Učenik 5. razreda

Elena Sergeevna Papotina

naučni direktor:

učitelj MBOU Doschatinskaya srednje škole

Roshina Lyudmila Valerievna

Region Nižnji Novgorod

r / p Dooschatoe

2016

anotacija

Svrha ovog radaotkriti sposobnost rasuđivanja i donošenja ispravnih zaključaka prilikom rješavanja logičkih zadataka.Ovezadaci su zabavni i ne zahtijevaju veliku zalihu matematičkog znanja, pa privlače i one učenike koji matematiku baš i ne vole.Rad je postavio sljedeće zadatke:

1) upoznavanje sa pojmovima "logika" i "matematička logika";

2) proučavanje osnovnih metoda rešavanja logičkih zadataka;

3) proučavanje sposobnosti rješavanja logičkih zadataka učenika 5-7 razreda.

Metode istraživanja ovog rada su:

Prikupljanje i proučavanje informacija.

Generalizacija eksperimentalnog i teorijskog materijala.

Hipoteza : učenici naše škole umeju da rešavaju logičke zadatke.

U toku pisanja rada istražene su vrste i metode rješavanja logičkih zadataka. Sa učenicima srednjeg nivoa rađen je praktičan rad o tome kako su sposobni rješavati logičke probleme. Rezultati rada su pokazali da se svi učenici ne mogu nositi sa logičkim problemima.Najčešće, sposobnosti školaraca ostaju neotkrivene za sebe, nisu sigurni u svoje sposobnosti, ravnodušni su prema matematici.Za takve učenike predlažem korištenje logičkih zadataka. Ovi zadaci se mogu razmatrati u krugu i vannastavnim aktivnostima.

2.3 Metoda Eulerovih krugova

Ova metodaje još jedan vizuelni i prilično zanimljiv način rješavanja logičkih problema. Ova metoda se zasniva na konstrukciji čuvenih Euler-Vennovih krugova,problemi u kojima je potrebno pronaći neki presek skupova ili njihovu uniju, posmatrajući uslove problema... Pogledajmo primjer korištenja ove metode.

Rešimo problem 6:

Od 52 školarca, 23 skuplja značke, 35 markice, a 16 i značke i marke. Ostali nisu zainteresovani za prikupljanje. Koliko školaraca nije zainteresovano za kolekcionarstvo?

Rješenje. Nije tako lako razumjeti stanje ovog problema. Ako zbrojimo 23 i 35, dobijemo više od 52. To je zbog činjenice da smo ovdje dva puta prebrojali neke školarce, odnosno one koji skupljaju bedževe i markice.Da bismo olakšali diskusiju, koristimo Ojlerove krugove

Na slici je prikazan veliki krugoznačava dotična 52 učenika; krug 3 predstavlja školarce koji skupljaju bedževe, a krug M predstavlja školarce koji skupljaju markice.

Veliki krug razbijen je krugovima 3 i M na nekoliko područja. Presjek krugova 3 i M odgovara školarcima koji skupljaju i bedževe i pečate (Sl.). Dio kruga 3 koji ne pripada krugu M odgovara da školarci skupljaju samo bedževe, a dijelu kruga M koji ne pripada krugu 3, školarci skupljaju samo markice. Slobodni dio velikog kruga označava školarce koji nisu zainteresirani za kolekcionarstvo.

Mi ćemo dosljedno ispunjavati našu šemu, upisujući odgovarajući broj u svako područje. Prema stanju, i značke i pečate skuplja 16 ljudi, stoga ćemo u raskrsnici krugova 3 i M upisati broj 16 (Sl.).

Pošto bedževe skuplja 23 školarca, a bedževe i pečate - 16 školaraca, samo bedževe skuplja 23 - 16 = 7 osoba. Na isti način, samo 35 - 16 = 19 ljudi skuplja marke. Zapišimo brojeve 7 i 19 u odgovarajuća područja dijagrama.

Sa slike se vidi koliko ljudi skuplja. Saznati,potrebno je sabrati brojeve 7, 9 i 16. Dobijamo 42 osobe. To znači da 52 - 42 = 10 školaraca i dalje ne želi sakupljati. Ovo je odgovor na problem; može se zapisati u slobodno polje velikog kruga.

Ojlerova metoda je neophodna za rješavanje nekih problema, a također uvelike pojednostavljuje rezonovanje.

2.4 Metoda blok dijagrama

Rješenje. Formulirajmo rješenje u obliku blok dijagrama:

Odgovor: 18 opcija.

2.5 Zadaci za istinitost

Zadaci u kojima je potrebno utvrditi istinitost ili netačnost iskaza nazivat će se zadaci istine.

Problem 7 ... Trojica prijatelja Kolja, Oleg i Petja igrali su se u dvorištu, a jedan od njih je loptom slučajno razbio stakleni prozor. Kolja je rekao: "Nisam ja razbio staklo." Oleg je rekao: "Petya je razbila staklo." Kasnije se pokazalo da je jedna od ovih izjava tačna, a druga nije. Koji dečko je razbio staklo?

Rješenje. Pretpostavimo da je Oleg rekao istinu, a onda je Kolja rekao istinu, a to je u suprotnosti sa stanjem problema. Shodno tome, Oleg je rekao laž, a Kolja - istinu. Iz njihovih izjava proizilazi da je staklo razbio Oleg.

Problem 8. Četiri učenika - Vitya, Petya, Yura i Sergej - zauzeli su četiri prva mjesta na matematičkoj olimpijadi. Na pitanje koja su mesta zauzeli, odgovore su dobili:

a) Petja - drugi, Vitja - treći;

b) Sergej - drugi, Petja - prvi;

c) Jura je drugi, Vitja je četvrti.

Navedite ko je zauzeo koje mjesto, ako je samo jedan dio tačan u svakom odgovoru.

Rješenje. Pretpostavimo da je tvrdnja "Petar - II" tačna, tada su obje izjave druge osobe netačne, a to je u suprotnosti sa uslovom problema. Pretpostavimo da je izjava "Sergei - II" tačna, tada su obje izjave prvog lica netačne, a to je u suprotnosti sa uslovom problema. Pretpostavimo da je izjava "Jura - II" tačna, tada je prva izjava prve osobe netačna, a druga tačna. I prva izjava druge osobe je pogrešna, a druga je tačna.

Odgovor: prvo mjesto - Petya, drugo mjesto - Yura, treće mjesto - Vitya, četvrto mjesto - Sergej.

2.6 Zadaci riješeni od kraja.

Postoji ova vrsta logičkog problema koji se rješava od kraja. Razmotrimo primjer rješavanja takvih problema.

Problem 9. Vasja je smislio broj, dodao mu 5, zatim podelio zbir sa 3, pomnožio sa 4, oduzeo 6, podelio sa 7 i dobio broj 2. Šta je Čilo Vasja imao na umu.

Rješenje: 2 7 = 14

14+6=20

20˸4 = 5

5 3 = 15

15-5=10

Odgovor: Vasja je smislio broj 10.

Poglavlje 3. Učenje sposobnosti rješavanja logičkih problema.

U praktičnom dijelu istraživačkog rada odabrao sam logičke probleme tipa: problemi riješeni od kraja; ko je ko?; problemi sa rečima.

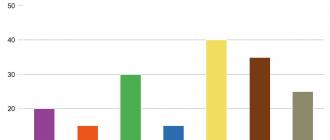
Zadaci su odgovarali nivou znanja 5., 6. i 7. razreda. Učenici su rješavali ove probleme, a ja sam analizirao rezultate (Sl. 1). Razmotrimo dobijene rezultate detaljnije.

* Za 5. razred predloženi su sljedeći zadaci:

Problem broj 1. Problem rešen od kraja.

Smislio sam broj, pomnožio sa dva, dodao tri i dobio 17. Na koji broj mislim?

Problem broj 2. Problemi poput "Ko je ko?"

Katja, Sonja i Liza se prezivaju Vasnjecov, Ermolajev i Kuznjecov. Koje prezime ima svaka djevojka ako su Sonja, Liza i Ermolaeva članovi matematičkog kruga, a Liza i Kuznjecova se bave muzikom?

Problem broj 3. Tekst zadatka.

Školskoj sportskoj olimpijadi prisustvovalo je 124 učesnika, od čega 32 više dječaka nego djevojčica. Koliko je dječaka i djevojčica učestvovalo na olimpijadi.

Većina učenika petog razreda snašla se sa problemom tipa: "riješeno od kraja". Takvi zadaci nalaze se u udžbenicima 5-6 razreda.S obzirom na vrstu tektonskih zadataka, ovi zadaci su složeniji, o tome je trebalo špekulirati, samo 5 ljudi se s tim snašlo.(sl. 2)

* Za 6. razred predloženi su sledeći zadaci:

Problem broj 1. Problem rešen od kraja.

Zamislio sam broj, oduzmem 57, podijelim sa 2 i dobijem 27. Na koji broj mislim?

Problem broj 2. Problemi poput "Ko je ko?"

Atos, Porthos, Aramis i D'Artagnan su četiri talentovana mlada mušketira. Jedan se najbolje bori mačevima, drugom nema premca u prsa u prsa, treći najbolje pleše na balovima, četvrti gađa pištoljima bez promašaja. O njima se zna sledeće:

Atos i Aramis su na balu gledali svog prijatelja, divnog plesača.

Porthos i najbolji strijelac jučer su sa divljenjem pratili borbu prsa u prsa.

Strelac želi da pozove Atos u posetu.

Porthos je bio veoma velik, tako da ples nije bio njegov element.

ko šta radi?

Problem broj 3. Tekst zadatka. Jedna polica ima 5 puta više knjiga od druge. Nakon što je 12 knjiga prebačeno sa prve police na drugu, broj knjiga na policama se izjednačio. Koliko je knjiga prvobitno bilo na svakoj polici?

Među učenicima 6. razreda, u broju od 18 osoba, 1 osoba se snašla sa svim zadacima. Svi učenici 6. razreda su se nosili sa problemom tipa: "riješeno od kraja". Sa problemom broj 2, kao što je "Ko je ko?" 4 osobe su to uradile. Samo jedna osoba se snašla sa tekstualnim zadatkom(sl. 3).

* Za 7. razred predloženi su sledeći zadaci:

Problem broj 1. Problem rešen od kraja.

Zamislio sam broj, dodao mu 5, zatim podijelio zbir sa 3, pomnožio sa 4, oduzeo 6, podijelio sa 7 i dobio broj 2. Na koji sam broj mislio.

Problem broj 2. Problemi poput "Ko je ko?"

Vanja, Petja, Saša i Kolja imaju prezimena koja počinju na slova V, P, C i K. Poznato je da su 1) Vanja i S. odlični učenici; 2) Petya i V. - učenici C razreda; 3) U rastu iznad P .; 4) Kolya je niži od P .; 5) Sasha i Petya imaju istu visinu. Kojim slovom počinju prezimena svakog od njih?

Problem broj 3. Metoda rasuđivanja.

Stigla je ekipa da popravi školu u kojoj je bilo 2,5 puta više molera nego stolara. Ubrzo je predradnik u brigadu uključio još 4 molera, a dva stolara prebacio na drugi objekat. Kao rezultat toga, u brigadi je bilo 4 puta više molera nego stolara. Koliko je molera, a koliko stolara u početku bilo u timu?

Među učenicima 7. razreda, u broju od 20 osoba, 1 osoba se snašla sa svim zadacima.Sa problemom tipa: "riješeno od kraja" riješilo se 13 učenika. WITHjedan učenik se snašao sa tekstualnim zadatkom (sl. 4).

Zaključak

U toku istraživačkog rada na proučavanju metoda za rješavanje logičkih problema. Cilj i zadatke koje sam postavila smatram ispunjenim. U prvom poglavlju sam se upoznao sa pojmom logike kao nauke, glavnim fazama njenog razvoja i naučnicima koji su njeni osnivači. U drugom poglavlju sam naučio različite metode rješavaju logičke probleme i analiziraju ih na konkretnim primjerima. Ja sam razmatrao sljedeće metode: mmetoda zaključivanja, metoda tabela, metoda grafova, metoda blok dijagrama, metoda Ojlerovih krugova, istinski problemi, metoda rješavanja problema s kraja.U trećem poglavlju proveo sam praktično istraživanje među učenicima 5-7 razreda, testirajući njihovu sposobnost rješavanja logičkih zadataka. Moje istraživanje je pokazalo sljedeće. Zadaci s kojima se većina učenika snašla su zadaci koji se rješavaju do kraja. Sa zadatkom "Ko je ko?" (metod tabela) polovina učenika se snašla. Problem teksta (metoda zaključivanja) riješio je samo najmanji broj ljudi. Vjerujem da je moja hipoteza djelimično potvrđena, jer je polovina učenika teško rješavala logičke zadatke.

Logički zadaci pomažu u razvoju logičkog i maštovitog razmišljanja.Svako normalno dijete ima želju za znanjem, želju da se testira. Najčešće, sposobnosti školaraca ostaju neotkrivene za sebe, nisu sigurni u svoje sposobnosti, ravnodušni su prema matematici.Za takve učenike predlažem korištenje logičkih zadataka. Ovi zadaci se mogu razmatrati u krugu i vannastavnim aktivnostima. Trebali bi biti dostupni, probuditi oštroumnost, zaokupiti njihovu pažnju, iznenaditi, probuditi ih na aktivnu maštu i samostalnu odluku. Također vjerujem da nam logika pomaže da se nosimo sa svim poteškoćama u životu, a sve što radimo treba da bude logički smisleno i izgrađeno. Logičke i logičke probleme susrećemo ne samo u školi na časovima matematike, već iu drugim predmetima.

Književnost

Vilenkin N. Ya. Matematika, 5. razred, Mnemosyne, Moskva: 2015. 45 strana

Vilenkin N. Ya. Matematika, 5. razred, Mnemosyne, Moskva: 2015. 211 pp.

Orlova E. Metode rješenja logički i brojčani problemi //

Matematika. -1999. br. 26. - S. 27-29.

Tarski A. Uvod u logiku i metodologiju deduktivnih nauka - Moskva ,: 1948.

Internet resursi:

http: //wiki. Predajem.

Rice. 3 Analiza radova 6. razreda.

Rice. 4 Analiza rada 7. razreda

Pošaljite svoj dobar rad u bazu znanja je jednostavno. Koristite obrazac ispod

Studenti, postdiplomci, mladi naučnici koji koriste bazu znanja u svom studiranju i radu biće vam veoma zahvalni.

Objavljeno na http://www.allbest.ru/

DIPLOMSKI RAD

Tema diplomskog rada

„Upotreba elemenata matematičke logike u nastavi matematike u osnovni razredi»

početnik u matematičkoj logici

Uvod

Poglavlje 1. Teorijske osnove izučavanja elemenata matematičke logike u osnovnoj školi

1.1 Koncept logičke strukture matematičkih pojmova i rečenica

1.2 Proučavanje logike kao grane matematike

1.3 Logičko zaključivanje

Zaključci za 1. poglavlje

Poglavlje 2. Upotreba elemenata matematičke logike u nastavi matematike u osnovnim razredima

2.1 Upotreba elemenata logike u početnom kursu matematike

2.2 Psihološko-pedagoške osnove upotrebe elemenata matematičke logike prema metodi nastave i učenja "Perspektivna osnovna škola"

2.3 Sistem zadataka usmjerenih na formiranje koncepta "elemenata matematičke logike" među učenicima nakon završetka osnovne škole

Zaključci o poglavlju 2

Zaključak

Bibliografija

Prijave

Uvod

Trenutno, zemlja aktivno traži načine za poboljšanje matematičkog obrazovanja. Na osnovu Federalnog državnog obrazovnog standarda novog opšteg obrazovanja, učenici osnovnih škola moraju se pridržavati uslova za rezultate savladavanja osnovnih obrazovni program početni opšte obrazovanje na predmetu matematike:

1) koristi početna matematička znanja za opisivanje i objašnjenje okolnih objekata, procesa, pojava, kao i za procenu njihovih kvantitativnih i prostornih odnosa;

2) ovlada osnovama logičkog i algoritamskog mišljenja, prostorne imaginacije i matematičkog govora, merenja, preračunavanja, procene i vrednovanja, vizuelnog prikaza podataka i procesa, snimanja i izvršavanja algoritama;

3) umeti da usmeno i pismeno izvodi računske operacije sa brojevima i brojevnim izrazima, rešava rečne zadatke, ume da deluje u skladu sa algoritmom i gradi najjednostavnije algoritme, istražuje, prepoznaje i prikazuje geometrijske figure, radi sa tabelama, dijagramima , grafikoni i dijagrami, lanci, agregati, za predstavljanje, analizu i interpretaciju podataka.

Danas je matematičko obrazovanje dio srednjoškolskog obrazovnog sistema, a ujedno i svojevrsna samostalna faza obrazovanja. Novi sadržaj matematičkog obrazovanja usmjeren je uglavnom na formiranje kulture i samostalnosti mišljenja mlađih školaraca, elemente obrazovne aktivnosti matematičkim sredstvima i metodama. U toku obuke djeca treba da nauče opšte metode djelovanja, provođenje korak-po-korak kontrole i samoprocjene izvršenih aktivnosti kako bi se utvrdila usklađenost svojih akcija sa planiranim planom.

Zato se, ne slučajno, u matematičkim programima posebna pažnja poklanja formiranju algoritamskih, logičkih i kombinatornih linija, koje se razvijaju u procesu proučavanja aritmetičkih, algebarskih i geometrijskih dijelova programa.

U djelima matematičara A.N. Kolmogorov, A.I. Markushevich A.S. Joiner, A.M. Pyshkalo, P.M. Erdniev i saradnici su istakli temeljna pitanja unapređenja školskog matematičkog obrazovanja, posebno pitanja koja se odnose na jačanje logičke osnove školskog predmeta, uključujući elemente matematičke logike u njemu.

U posljednjoj deceniji, kada je škola ušla u proces modernizacije, uvode se u praksu novi standardi, tehnologije, metodike, razna nastavna sredstva, pitanje kontinuiteta u nastavi između inicijalne i osnovne faze postaje najvažnije. Prisustvo kompleta udžbenika je važna komponenta kontinuiteta između ovih koraka. Prema A.A. Stolaru je „potreban mentalni, logički program koji se mora implementirati u osnovnoj i srednjoj školi“.

Istraživanje psihologa i pedagoga V.V. Vygotsky, L.V. Zankova, V.V. Davidov, N.M. Skatkina i drugi pokazuju da je pod određenim uslovima moguće postići ne samo visoki nivo znanja, sposobnosti i vještina, ali i opći razvoj. U tradicionalnoj nastavi razvoj se pojavljuje kao poželjan, ali daleko od predvidljivog proizvoda učenja.

Prema našem mišljenju, u psihološko-metodičkoj literaturi, problem formiranja elemenata matematičke logike kod učenika razmatra se djelimično, u odnosu na nastavu matematike u srednjoj školi.

Dakle, skup brojeva, počevši od prvih časova sveobuhvatne škole, predstavlja laboratoriju u kojoj je moguće kod učenika jasnije formirati vještine zaključivanja, koje su osnova za razjašnjavanje istinitosti ili neistinitosti ovog ili onog pristupa, ove ili one formulacije problema. Postavlja se pitanje: „Da li je takav zadatak glavni cilj procesa nastave matematike u školi i koliki udio ovog problema otpada na osnovnu školu?“ Odgovor na ovo pitanje može se dobiti tek nakon detaljne analize nastavnog plana i programa i udžbenika iz matematike za I-IV razred.

Aktuelnost problema je unapređenje sadržaja nastave matematike u osnovnim razredima kako bi se kod mlađih učenika formirali elementi matematičke logike.

Svrha studije razmotriti proučavanje elemenata matematičke logike kao dio predmeta matematike u nastavi matematike od 1. do 4. razreda i razvijati nastavno-metodička sredstva za njegovu implementaciju.

Predmet proučavanja- proces izučavanja elemenata matematičke logike u nastavi matematike u osnovnoj školi.

Stavka- metode i sredstva formiranja elemenata matematičke logike kod učenika 1-4 razreda.

Istraživačka hipoteza leži u činjenici da postoji mogućnost organizovanja procesa nastave matematike, čime ćemo, uz pripremu matematičkih znanja i vještina, svjesno i sistematski razvijati logičke vještine.

Za postizanje ovog cilja i implementaciju hipoteze utvrđeno je sljedeće ciljevi istraživanja:

1. Dati pojam logičke strukture matematičkih pojmova i rečenica;

2. Proučavati logiku kao nauku i granu matematike;

3. Saznajte šta je logičko rezonovanje i dajte njihove definicije;

4. Analizirati obrazovne standarde, nastavne planove i programe i postojeće školske udžbenike iz matematike sa stanovišta logičkog razvoja učenika;

5. Otkriti psihološke, pedagoške i metodološke osnove formiranje elemenata matematičke logike kod djece u procesu nastave matematike u osnovnim razredima;

6. Provesti eksperimentalno istraživanje kako bi se ispitala efikasnost razvijenih metoda u uslovima osnovne škole.

Teorijsku i metodološku osnovu studije činile su: glavne odredbe dijalektičko-materijalističke filozofije i na njihovoj osnovi razvijena doktrina lično-aktivnog pristupa učenju (A.S. Vigotski, A.N. Leontijev, S.L. Rubinštajn, itd.); početne odredbe teorije razvojnog učenja (V.V.Davydov, L.V. Zankov, N.A. Menchinskaya, D.B. Elkonin, N.V. Yakimanskaya, itd.); fundamentalne ideje metodologa-matematičara (A.M. Pyshkalo, P.M. Erdniev).

Poglavlje 1. Teorijske osnove izučavanja elemenata matematičke logike u osnovnoj školi

1.1 Koncept logičke strukture matematičkih pojmova i rečenica

Izučavajući matematiku u školi, potrebno je savladati određeni sistem pojmova, rečenica i dokaza, ali da bi se savladao ovaj sistem i potom uspješno primjenjivala stečena znanja i vještine, podučavajući mlađe učenike i rješavajući problem njihovog razvoja putem matematike, morate razumjeti koje su karakteristike matematičkih pojmova, kako su raspoređene definicije, rečenice koje izražavaju svojstva pojmova i dokazi.

Takvo znanje je neophodno za nastavnika osnovni razredi jer on prvi uvodi djecu u svijet matematičkog znanja, a od toga koliko će to kompetentno i uspješno obavljati zavisi i odnos djeteta prema nastavi matematike u budućnosti.

Proučavanje ovog materijala povezano je sa ovladavanjem teoretsko-teoretskim jezikom, koji će se koristiti ne samo pri razmatranju logičke strukture matematičkih pojmova, rečenica i dokaza, već i pri izgradnji cijelog kursa.

Pojmovi koji se izučavaju u osnovnom predmetu matematike obično su predstavljeni u obliku četiri grupe. Prvi uključuje pojmove vezane za brojeve i operacije nad njima: broj, sabiranje, pojam, više itd. Lopov uključuje algebarske pojmove: izraz, jednakost, jednačina itd. Treću čine geometrijski pojmovi: prava, segment, trougao, itd. Četvrtu grupu čine pojmovi vezani za veličine i njihovo mjerenje.

Za proučavanje takvog obilja vrlo različitih koncepata, potrebno je imati ideju o konceptu kao logičkoj kategoriji i karakteristikama matematičkih koncepata.

U logici, pojmovi se smatraju oblikom mišljenja koji odražava objekte (predmete ili pojave) u njihovim bitnim i općim svojstvima. Jezički oblik pojma je riječ ili grupa riječi.

Misliti o nekom objektu znači biti u stanju razlikovati ga od drugih sličnih objekata. Matematički koncepti imaju niz posebnosti. Glavna stvar je da matematički objekti u odnosu na koje se formiraju koncepti, zapravo, ne postoje. Sve matematičke objekte stvara ljudski um. Idealni objekti koji odražavaju stvarne objekte ili pojave.

Na primjer, u geometriji se proučava oblik i veličina objekata, ne uzimajući u obzir druga svojstva: boju, masu, tvrdoću itd. Oni su od svega toga odvučeni, apstrahovani. Stoga se u geometriji umjesto riječi "objekat" kaže "geometrijska figura".

Apstrakcija rezultira takvim matematičkim konceptima kao što su "broj" i "veličina".

Općenito, matematički objekti postoje samo u čovjekovom razmišljanju iu onim znakovima i simbolima koji čine matematički jezik.

Proučavajući prostorne oblike i kvantitativne odnose materijalnog svijeta, matematika ne koristi samo različite metode apstrakcije, već i sama apstrakcija djeluje kao višestepeni proces.

Pojava u matematici novih pojmova, a time i novih pojmova koji označavaju ove pojmove, pretpostavlja njihovu definiciju.

Definicijom se obično naziva rečenica koja pojašnjava suštinu novog pojma (ili oznake). U pravilu to rade na osnovu prethodno uvedenih koncepata.

Budući da je definicija pojma u smislu rodne i vrste razlike u suštini uslovni dogovor o uvođenju novog pojma ili zamjeni bilo kojeg skupa poznatih pojmova, nemoguće je reći o definiciji da li je istinita ili netačna; nije ni dokazano ni opovrgnuto. Ali kada formuliraju definicije, oni se pridržavaju brojnih pravila:

· Definicija mora biti proporcionalna. To znači da se obim definisanih i definišnih pojmova moraju poklapati. Ovo pravilo proizilazi iz činjenice da su definisani i definisani koncepti međusobno zamenljivi;

· U definiciji (ili njihovom sistemu) ne bi trebalo biti začaranog kruga. To znači da se ne može definirati pojam kroz sebe (pojam koji definira ne bi trebao sadržavati definirani pojam) ili ga definirati kroz drugi, koji se, pak, kroz njega može definirati. Budući da se u matematici ne razmatraju samo pojedinačni pojmovi. A njihov sistem, ovo pravilo zabranjuje začarani krug u sistemu definicija;

· Definicija treba da bude jasna. Ovo na prvi pogled nije očigledno pravilo, ali mnogo znači. Prije svega, potrebno je da značenje pojmova uključenih u definitivni koncept bude poznato do trenutka uvođenja definicije novog pojma. Uslovi za jasnoću definicije takođe uključuju preporuku da se u razlikovanje vrsta uključi samo onoliko svojstava koliko je neophodno i dovoljno da se definisani objekti razlikuju iz opsega generičkog koncepta.

Prilikom izučavanja matematike u osnovnim razredima rijetko se koriste definicije kroz rodne i vrste. Postoji mnogo koncepata u početnom kursu matematike.

Prilikom izučavanja matematike u osnovnoj školi najčešće se koriste tzv. implicitne definicije. U njihovoj strukturi nemoguće je razlikovati definirano i definirajuće. Među njima se razlikuju kontekstualni i ostenzivni.

U kontekstualnim definicijama, sadržaj novog pojma otkriva se kroz odlomak teksta, kroz kontekst, kroz analizu konkretne situacije. Opisivanje značenja uvedenog pojma. Kroz kontekst se uspostavlja veza između definisanog pojma i drugih poznatih, te se na taj način posredno otkriva njegov sadržaj. Primjer kontekstualne definicije bi bila definicija jednadžbe i njenog rješenja.

Ostenzivne definicije su definicije po prikazu. Koriste se za uvođenje pojmova demonstriranjem objekata koje ti pojmovi označavaju. Na primjer, u osnovnoj školi koncepti jednakosti i nejednakosti mogu se definirati na ovaj način.

Proučavanje stvarnih procesa, matematički opisi, koriste se kao prirodni verbalni jezik i simboličko značenje. Opisi se grade pomoću rečenica. Ali, da će matematičko znanje biti tačan, adekvatan odraz stvarnosti koja nas okružuje, ove rečenice moraju biti istinite. Svaku matematičku tezu karakteriše sadržaj i logička forma (struktura) i sadržaj je neraskidivo povezan sa formom, te je prvu nemoguće razumeti, a ne razumeti drugu.

1) Broj 12 je paran;

Vidimo da se rečenice koje se koriste u matematici mogu napisati i na prirodnom (ruskom) jeziku i na matematičkom, koristeći simbole. Za rečenice 1,4,5 i 6 možemo reći da sadrže tačne informacije, a za rečenicu 2 – netačne. Što se tiče rečenice x +5 = 8, generalno je nemoguće reći da li je tačna ili netačna. Gledanje na rečenicu iz perspektive istinite ili lažne dovelo je do koncepta iskaza.

1.2 Proučavanje logike kao grane matematike

Logika je jedna od najstarijih nauka. Trenutno nije moguće tačno utvrditi ko se, kada i gdje prvi put obratio onim aspektima mišljenja koji čine predmet logike. Kako navodi A.A. Ivin. , pojedinačni izvori logičke doktrine mogu se naći u Indiji, na kraju 2. milenijuma pr. međutim, ako govorimo o nastanku logike kao nauke, odnosno o manje-više sistematizovanom korpusu znanja, onda bi bilo pošteno smatrati veliku civilizaciju antičke Grčke domovinom logike. Bilo je ovdje u 5. - 4. vijeku prije nove ere. U periodu naglog razvoja demokratije i s tim povezanog neviđenog oživljavanja društvenog i političkog života, radovi Demokrita, Platona i Sokrata postavili su temelje ove nauke. Predak, "otac" logike, s pravom se smatra najvećim misliocem antike. Platonov učenik - Aristotel (384-322 pne). upravo je on u svojim radovima, ujedinjenim opštim imenom "Organon" (sredstvo spoznaje), prvi put temeljito analizirao i opisao glavne logičke forme i pravila rasuđivanja, odnosno: oblike zaključaka iz tzv. - pod nazivom kategorički sudovi - kategorički silogizam ("Prva analitika"), formulisao je osnovne principe naučnih dokaza ("Druga analitika"), dao analizu značenja nekih vrsta iskaza ("O tumačenju"), naveo glavne pristupi razvoju doktrine koncepta ("Kategorije"). Aristotel je takođe posvetio ozbiljnu pažnju razotkrivanju raznih vrsta logičkih grešaka i sofističkih metoda u sporovima („O sofističkim pobijanjima“).

Logika ima dugu i bogatu istoriju, neraskidivo povezana sa istorijom razvoja društva u celini.

Nastanku logike kao teorije prethodila je praksa razmišljanja hiljadama godina unazad. Razvojem radnih, materijalnih i proizvodnih aktivnosti ljudi postepeno je dolazilo do poboljšanja i razvoja njihovih misaonih sposobnosti, prvenstveno sposobnosti apstrakcije i zaključivanja. A to je, prije ili kasnije, ali neminovno moralo dovesti do toga da je predmet istraživanja samo mišljenje sa svojim oblicima i zakonima.

Kako navodi A.A. Ivin. , istorija svedoči da se individualni logički problemi javljaju pred mentalnim pogledom osobe već pre više od 2,5 hiljade godina - prvo u staroj Indiji i staroj Kini. Onda prebole kompletan razvoj u staroj Grčkoj i Rimu. Tek postepeno se uobličava manje-više harmoničan sistem logičkog znanja, formira se nezavisna nauka.

Koji su razlozi za pojavu logike? Ivin A.A. smatra da postoje dva glavna. Jedna od njih je rađanje i početni razvoj nauka, posebno matematike. Ovaj proces datira iz 6. veka. BC. a najpotpunije je razvijena u staroj Grčkoj. Rođena u borbi protiv mitologije i religije, nauka je bila zasnovana na teorijskom razmišljanju, uključujući zaključke i dokaze. Otuda - potreba za proučavanjem prirode samog mišljenja kao sredstva saznanja.

Prema V. I. Kurbatovu , logike i nastao je, pre svega, kao pokušaj da se identifikuju i potkrepe zahtevi koje naučno mišljenje mora da zadovolji da bi njegovi rezultati odgovarali – stvarnosti.

Drugi, možda čak i više važan razlog- To je razvoj govorništva, uključujući i sudsko, koje je procvjetalo u uslovima antičke grčke demokratije. Najveći rimski govornik i naučnik Ciceron (106-43. p.n.e.), govoreći o moći govornika, vlasnika „božanskog dara“ – elokvencije, naglašava: „On može sigurno ostati čak i među naoružanim neprijateljima, zaštićen ne toliko s njegov štap, koliko po naslovu govornika; svojom riječju može izazvati ogorčenje sugrađana i srušiti kaznu na krivce za zločin i prevaru, a nevine snagom svog talenta spasiti od suda i kazne; u stanju je da navede plašljiv i neodlučan narod na junačko djelo, u stanju je da ga izvede iz zablude, umije da se raspali protiv zlikovaca i smiri žamor protiv dostojnih ljudi; konačno zna kako, jednom svojom riječju, da uzbudi i smiri sve ljudske strasti kada to okolnosti slučaja zahtijevaju."

Prema A. A. Ivinu, najveći starogrčki filozof i naučnik-enciklopedista Aristotel (384-322 pne) smatra se osnivačem logike - ili, kako se ponekad kaže, "ocem logike". Međutim, treba imati na umu da je prvi prilično detaljan i sistematičan prikaz logičkih problema zapravo dao raniji starogrčki filozof i prirodnjak Demokrit (460. - oko 370. godine prije Krista). Među njegovim brojnim djelima bila je i opsežna rasprava u tri knjige "O logičkom, ili o kanonima". Ovdje je otkrivena ne samo suština znanja, njegovi osnovni oblici i kriteriji istine, već je prikazana i ogromna uloga logičkog rasuđivanja u znanju, te je data klasifikacija sudova. Određene vrste inferencijalnog znanja bile su oštro kritizirane i učinjen je pokušaj da se razvije induktivna logika – logika eksperimentalnog znanja. Nažalost, ova Demokritova rasprava, kao i sve druge, nije stigla do nas.

Nova, viša faza u razvoju logike počinje u 17. veku. Ova faza je organski povezana sa stvaranjem u svojim okvirima, zajedno sa deduktivnom logikom, induktivnom logikom. Ona odražava različite procese sticanja opšteg znanja na osnovu sve više akumuliranog empirijskog materijala. Potrebu za takvim znanjem najpotpunije je shvatio i izrazio u svojim spisima istaknuti engleski filozof i prirodnjak F. Bacon (1561-1626). Postao je osnivač induktivne logike. "...logika koju sada imamo beskorisna je za otkrivanje znanja", izrekao je svoju strogu rečenicu. Stoga, kao da je u suprotnosti sa starim Aristotelovim "Organonom", Bekon je napisao "Novi organon...", gde je izneo induktivnu logiku. U njemu je glavnu pažnju posvetio razvoju induktivnih metoda za utvrđivanje uzročne zavisnosti pojava. To je velika zasluga Bacona. Međutim, doktrina indukcije koju je on stvorio, ironično, nije bila negacija prethodne logike. I njeno dalje obogaćivanje i razvoj. To je doprinijelo stvaranju generalizirane teorije zaključivanja. I to je prirodno, jer, kao što će biti pokazano u nastavku, indukcija i dedukcija ne isključuju, već se pretpostavljaju i nalaze se u organskom jedinstvu.

Poznati doprinos razvoju tradicionalne formalne logike dali su ruski naučnici. Dakle, već u prvim raspravama o logici počevši od otprilike X vijeka. činjeni su pokušaji da se nezavisno komentarišu dela Aristotela i drugih naučnika. Originalni logički koncepti u Rusiji razvijeni su u 18. veku. a vezuju se prvenstveno za imena M. Lomonosova (1711-1765) i A. Radiščova (1749-1802). Procvat logičkog istraživanja u našoj zemlji datira s kraja 19. vijeka.

Grandiozan pokušaj da se razvije integralni sistem nove, dijalektičke logike, preduzeo je nemački filozof - G. Hegel (1770-1831). U svom temeljnom djelu "Nauka o logici" on je prije svega otkrio temeljnu kontradikciju između dostupnih logičkih teorija i stvarne prakse mišljenja, koja je do tada dostigla značajne visine.

Kako ističe V. I. Kurbatov, Hegel je preispitao prirodu mišljenja, njegove zakone i forme. S tim u vezi, došao je do zaključka da „dijalektika sačinjava prirodu samog mišljenja, da u svojstvu razuma mora pasti u poricanje samog sebe, u kontradikciju“. Mislilac je svoj zadatak vidio u pronalaženju načina da razriješi ove kontradikcije. Hegel je oštro kritizirao staru, običnu logiku zbog njene povezanosti s metafizičkim metodom spoznaje. Ali u ovoj kritici otišao je tako daleko da je odbacio njene principe zasnovane na zakonu identiteta i zakonu kontradikcije.

Ivin A.A. kaže da su problemi dijalektičke logike, njen odnos sa formalnim našli dalju konkretizaciju i razvoj u radovima nemačkih filozofa i naučnika K. Marxa 1818-1883) i F. Engelsa (1820-1895). Koristeći najbogatiji misaoni materijal akumuliran od strane filozofije, prirodnih i društvenih nauka, stvorili su kvalitativan novi, dijalektičko-materijalistički sistem, koji je oličen u djelima kao što su "Kapital" K. Marxa, "Anti-Duhring" i "Dijalektika prirode". “ od F. Engelsa. sa ovih opštih filozofskih pozicija, Marx i Engels su vrednovali posebnu "doktrinu mišljenja i njenih zakona" - logiku i dijalektiku. Nisu poricali važnost formalne logike, nisu je smatrali "besmislicom", ali su naglašavali njen istorijski karakter. Tako je Engels primetio da je teorijsko razmišljanje svake ere istorijski proizvod koji uzima različita vremena vrlo razne forme a istovremeno i veoma različit sadržaj. „Shodno tome, nauka o mišljenju, kao i svaka druga nauka, jeste istorijska nauka, nauka o istorijskom razvoju ljudskog mišljenja”.

Poslednjih decenija u našoj zemlji učinjeno je mnogo plodonosnih pokušaja da se dijalektička logika sistematski prikaže. Razvoj se odvija u dva glavna pravca. S jedne strane, to je razotkrivanje obrazaca refleksije u ljudskom razmišljanju razvojne stvarnosti, njenih objektivnih kontradiktornosti, as druge, razotkrivanje obrazaca razvoja samog mišljenja, njegove vlastite dijalektike.

U uslovima naučne i tehnološke revolucije, kada nauke prelaze na nove, dublje nivoe znanja i kada se povećava uloga dijalektičkog mišljenja, potreba za dijalektičkom logikom sve više raste. Dobija nove podsticaje za svoj dalji razvoj.

Istinsku revoluciju u logičkim istraživanjima izazvalo je stvaranje u drugoj polovini 19. stoljeća matematičke logike, koja se nazivala i simboličkom i označila je novu, modernu etapu u razvoju logike.

Počeci ove logike mogu se pratiti već kod Aristotela, kao i kod njegovih sljedbenika, stoika u obliku elemenata predikatske logike i teorije modalnih zaključaka, kao i logike propozicija. Međutim, sistematski razvoj njenih problema datira iz mnogo kasnijeg vremena.

Kako A.A. Ivin ističe, sve veći napredak u razvoju matematike i prodor matematičkih metoda u druge nauke već u drugoj polovini 17. veka snažno su pokrenuli dva fundamentalna problema. S jedne strane, ovo je primjena logike za razvoj teorijske osnove teorija matematike, a s druge strane matematiizacija same logike kao nauke. Najdublji i najplodniji pokušaj rješavanja nastalih problema poduzeo je istaknuti njemački filozof i matematičar G. Leibniz (1646-1416). Tako je postao, u suštini, pionir matematičke logike. Leibniz je sanjao o vremenu kada naučnici neće raditi empirijska istraživanja, već računati s olovkom u rukama. Za to je nastojao izmisliti univerzalni simbolički jezik, pomoću kojeg bi se svaka empirijska nauka mogla racionalizirati. Nova saznanja, po njegovom mišljenju, biće rezultat logičkog proračuna - računice.

Prema V.I. Kurbatovu, Leibnizove ideje dobile su određeni razvoj u 18. vijeku i prvoj polovini 19. stoljeća. Međutim, najpovoljniji uslovi za snažan razvoj simboličke logike pojavili su se tek u drugoj polovini 19. veka. Do tog vremena matematiizacija nauka je posebno značajno napredovala, a u samoj matematici su se pojavili novi fundamentalni problemi njenog opravdanja. Engleski naučnik, matematičar i logičar Žd. Boulle (1815-1864) je u svojim djelima prvenstveno primjenjivao matematiku na logiku. Dao je matematičku analizu teorije zaključivanja, razvio logički račun ("Boolean algebra"). Njemački logičar i matematičar G. Frege (1848-1925) primjenjivao je logiku u proučavanju matematike. Pomoću proširenog predikatskog računa konstruisao je formalizovani sistem aritmetike.

Time je otvorena nova, moderna faza u razvoju logičkog istraživanja. Možda je najvažnija odlika ove faze razvoj i upotreba novih metoda za rješavanje tradicionalnih logičkih problema. To je razvoj i primjena vještačkog, takozvanog formaliziranog jezika - jezika simbola, tj. abecedni i drugi znakovi (otuda i najčešći naziv za modernu logiku - "simbolički").

Kako navodi A.A. Ivin. , razlikuju se dvije vrste logičkih računa: propozicijski račun i predikatski račun. U prvom slučaju dopuštena je apstrakcija od unutrašnje, konceptualne strukture sudova, au drugom se ova struktura uzima u obzir i, shodno tome, simbolički jezik se obogaćuje, dopunjuje novim znakovima.

Važnost simboličkih jezika u logici teško se može precijeniti. G. Frege ga je uporedio sa vrednošću teleskopa i mikroskopa. I njemački filozof G. Klaus (1912-1974) vjerovao je da stvaranje formaliziranog jezika ima isti značaj za tehniku ​​logičkog zaključivanja kao što je u sferi proizvodnje prijelaz od ručni rad na mašinu. Nastala na temelju tradicionalne formalne logike, simbolička logika, s jedne strane, pojašnjava, produbljuje i generalizira dosadašnje ideje o logičkim zakonima i oblicima, posebno u teoriji zaključaka, as druge strane proširuje i obogaćuje logičke probleme. više i više. Savremena logika je najsloženiji i najrazvijeniji sistem znanja. Uključuje mnoge pravce, odvojene, relativno nezavisne „logike“, sve potpunije izražavajući potrebe prakse i u konačnici odražavajući raznolikost složenosti okolnog svijeta, jedinstvo i raznolikost razmišljanja o ovom svijetu.

Simbolička logika nalazi sve širu primenu u drugim naukama - ne samo u matematici, već i u fizici, biologiji, kibernetici, ekonomiji, lingvistici. To dovodi do pojave novih grana znanja (matematike). Posebno je impresivna i jasna uloga logike u proizvodnji. Otvarajući mogućnost automatizacije procesa zaključivanja, omogućava prenošenje nekih funkcija mišljenja na tehničke uređaje. Njegovi rezultati nalaze sve širu primjenu u tehnologiji: u stvaranju relejno-kontaktnih kola, kompjutera, informaciono-logičkih sistema itd. Prema figurativnom izrazu jednog od naučnika, moderna logika nije samo „instrument” preciznog mišljenja, već i „misao” tačnog instrumenta, elektronskog automata. Dostignuća moderne logike koriste se iu pravnoj oblasti. Dakle, u forenzičkoj nauci, u različitim fazama proučavanja, vrši se logička i matematička obrada prikupljenih informacija.

Sve veće potrebe naučnog i tehnološkog napretka određuju dalji intenzivan razvoj moderne logike.

Ostaje da se kaže da su ruski naučnici dali važan doprinos razvoju sistema simboličke logike. Među njima se ističe P. Poretsky (1846-1907). Bio je prvi u Rusiji koji je počeo da drži predavanja iz matematičke logike. Matematička logika nastavlja da se razvija i sada.

Prema V.I.Kurbatovu, proučavanje matematičke logike disciplinuje um. Podsjećajući na poznatu izreku MV Lomonosova o matematici, možemo reći da matematička logika, više od bilo koje druge matematičke nauke, „dovodi um u red“.

Jezik bilo koje algebre sastoji se od skupa znakova koji se nazivaju abeceda ovog jezika.

Znakovi abecede, po analogiji sa znakovima abecede prirodnog jezika, nazivaju se slovima.

Postavlja se prirodno pitanje: koja slova treba da budu sadržana u abecedi jezika numeričke algebre?

Prije svega, očito, moramo imati slova za označavanje elemenata skupa - nosioca algebre, u ovom slučaju za označavanje brojeva, i varijable za elemente ovog skupa.

Primjenjujući decimalni brojevni sistem za označavanje brojeva, u abecedu numeričke algebre moramo uključiti deset slova koja se nazivaju brojevi: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, uz pomoć kojih se imena bilo kojih brojeva.

Kao numeričke varijable (varijable za brojeve bilo kojeg od skupova N, N0, Z, Q ili R), slova latinice a, b, c, x, y, z ili jedno od ovih slova sa indeksom, za primjer X1, koriste se, X2, Xn.

Ponekad se slova latinice koriste i kao numeričke konstante, odnosno kao nazivi brojeva (kada je u pitanju određeni, ali nije bitno koji, određeni broj). U ovom slučaju, početna slova latiničnog alfabeta a, b, c se obično koriste kao konstante, a posljednja slova x, y, z se koriste kao varijable.

Takođe su nam potrebna slova koja predstavljaju operacije. Za sabiranje i množenje koriste se dobro poznati znakovi (slova) + i *.

Osim toga, zagrade (lijeve i desne) igraju ulogu interpunkcije u jeziku algebre.

Dakle, abeceda jezika kojim se opisuje neka numerička algebra mora uključivati ​​skup koji se sastoji od četiri klase slova: I - brojevi od kojih se konstruišu imena brojeva; II - slova latinice - numeričke varijable ili konstante; III - znakovi rada; IV - zagrade.

Znakovi oduzimanja (-) i dijeljenja (:) mogu se unijeti definicijama odgovarajućih operacija.

Postepeno, abeceda numeričke algebre se dopunjuje drugim "slovima", a posebno se uvode znaci binarnih odnosa "jednako", "manje", "veće od".

Svi ovi znakovi uključeni su u abecedu matematičkog jezika, umjetnog jezika koji je nastao u vezi sa potrebom za preciznim, sažetim i nedvosmisleno shvaćenim formulacijama matematičkih zakona, pravila i dokaza.

Istorijski gledano, simbolika matematike nastajala je vekovima uz učešće mnogih istaknutih naučnika. Dakle, vjeruje se da je označavanje nepoznatih veličina u slovima koristio Diofant (III vek), široka upotreba velikih slova latinskog alfabeta u algebri počela je sa Viet (XVI vek). mala slova ovog alfabeta uvedena su za označavanje R. Descartesa (XVII vek). znak jednakosti (=) se prvi put pojavio u radovima engleskog naučnika R. Recorda (16. vek), ali je postao opšte korišćen tek u 18. veku. Znakovi nejednakosti (< , >) pojavio se početkom 17. vijeka, a uveo ga je engleski matematičar Gariot. I iako su znakovi "=", ">", "<» появились не так давно, сами понятия равенства и неравенства возникли в глубокой древности .

Izjava u matematici naziva se rečenica o kojoj pitanje ima smisla: da li je istinito ili netačno.

Mogu se donijeti različiti sudovi o konceptima i odnosu između njih. Jezički oblik presude su izjavne rečenice. Na primjer. U početnom kursu matematike možete pronaći sljedeće rečenice:

1) Broj 12 je paran;

4) u broju 15, desetina i 5 jedinica;

5) proizvod se ne menja permutacijom faktora;

6) Neki brojevi su djeljivi sa 3.

Vidimo da se rečenice koje se koriste u matematici mogu napisati i na prirodnom (ruskom) jeziku i na matematičkom, koristeći simbole. Za rečenice 1,4,5 i 6 možemo reći da sadrže tačne informacije, a za rečenicu 2 – netačne. Što se tiče rečenice x +5 = 8, generalno je nemoguće reći da li je tačna ili netačna.

Ako su dati iskazi A i B, onda se mogu koristiti za sastavljanje novih iskaza koristeći veznike "i", "ili", "ako ..., onda ...", "ili ... ili ..." , "ako i samo ako, ako ", kao i čestica" ne ". Na primjer, neka A znači izreku "Sada je sunčano", a B izreku "Sada je vjetrovito". Tada izjava "A i B" znači: "Sada je sunčano i vjetrovito", izjava "Ako nije A, onda nije B" - "Ako sada nije sunčano, onda nije ni vjetrovito."

Takvi iskazi se nazivaju složenim, a iskazi A i B uključeni u njih nazivaju se elementarni iskazi. Dvije složene tvrdnje A i B nazivaju se ekvivalentnima ako su istovremeno istinite i netačne pod bilo kojom pretpostavkom o istinitosti elementarnih iskaza uključenih u njih. U ovom slučaju napišite: A = B.

Od prvog časa iz matematike osnovci se suočavaju sa tvrdnjama, uglavnom istinitim. Oni se upoznaju sa takvim izjavama: 2> 1, 1< 2, 3 > 2, 2 + 1 = 3, 3 - 1= 2.

Ako je A neka izjava, onda, tvrdeći da je lažna, dobijamo novu izjavu, koja se zove odbijanje izjave A i označeni su simbolom B.

Dakle, ako je izjava istinita, onda je njena negacija lažna, i obrnuto. Ovaj zaključak se može napisati pomoću tabele u kojoj "I" znači tačan iskaz, a "L" - netačan. Tabele ove vrste se nazivaju tablice istinitosti (vidi Dodatak 2 na slici 1).

Neka su A i B dva elementarna iskaza. Kombinujući ih sa sindikatom "i", dobijamo novu izjavu koja se zove konjunkcija podaci izjave i označen je A? P. Unos A? B glasi: "A i B".

Po definiciji, konjunkcija dva iskaza je tačna ako i samo ako su oba iskaza tačna. Ako je barem jedan od njih netačan, onda je konjunkcija lažna (vidi Dodatak 2 na slici 2).

Razmotrite izjavu "7 - 4 = 3 i 4 je paran broj." To je spoj dvaju iskaza: "7 - 4 = 3" i "4 je paran broj." Pošto su obe tvrdnje tačne, onda je tačna i njihova konjunkcija.

Ako u konjunkciji A? Zamijenivši pozicije iskaza A i B, onda dobijamo konjunkciju oblika B? A. Iz tabele istinitosti može se videti da su formule A? B i B? A za različita značenja iskaza A i B, ili istovremeno tačne ili istovremeno netačne.

Dakle, oni su ekvivalentni, a za bilo koje izjave A i B imamo: A? B = B? A

Ova notacija izražava komutativno svojstvo konjunkcije, što vam omogućava da zamijenite termine konjunkcije.

Sastavljanje tablica istinitosti za (A? B)? C i A? (B? C), dobijamo da su za bilo koje istinite vrijednosti iskaza A, B, C istinite vrijednosti iskaza (A? B)? C i A? (B? C) utakmica.

Dakle (Ha? B)? C = A? (B? C).

Ova jednakost izražava svojstvo asocijativnosti veznika. Takva konjunkcija je istinita ako i samo ako su tačne sve tvrdnje uključene u nju.

Kombinovanjem dva elementarna iskaza A i B sa veznikom "ili", dobijamo novu izjavu koja se zove disjunkcija podaci izjave ... Disjunkcija iskaza A i B označava A? B i glasi "A ili B". Disjunkcija je lažna samo ako su oba iskaza iz kojih je formirana lažna; u svim ostalim slučajevima disjunkcija je tačna. Tabela istinitosti disjunkcije ima oblik (vidi Dodatak 2 na slici 3).

Za disjunkciju, kao i za konjunkciju, može se navesti više ekvivalencija. Za bilo koje A, B i C imamo:

A? B = B? A (komutativna disjunkcija);

(Ha? B)? C = A? (B? C) (disjunkciona asocijativnost).

Svojstvo asocijativnosti disjunkcije omogućava vam da izostavite zagrade i napišete A? V? C umjesto (A? B)? WITH.

Koristeći tablice istinitosti, to je lako utvrditi

(Ha? B)? C = (A? C)? (B? C)

(Ha? B)? C = (A? C)? (B? C)

Prva jednakost izražava distributivni zakon konjunkcije u odnosu na disjunkciju, a druga, distributivni zakon disjunkcije u odnosu na konjunkciju.

Operacije konjunkcije, disjunkcije i negacije povezane su sljedećim relacijama, čija se valjanost može utvrditi pomoću tablica istinitosti:

Ovi odnosi se nazivaju de Morganovim formulama.

Razmislite o složenom iskazu koji je formiran od dva elementarna koristeći riječi "ako ... onda ...".

Neka se, na primjer, daju izjave A: "Jučer je bila nedjelja" i B: "Nisam bio na poslu". Zatim složena izjava "Ako je jučer bila nedelja, onda nisam bio na poslu" ima formulu "Ako je A, onda B".

Zove se izreka "Ako A, onda B". implikacija izjava A, B i uz pomoć simbola zapisuju se na sljedeći način: A => B. Izjava A uključena u implikaciju A => B naziva se uslov implikacije, a iskaz B njen zaključak.

Prema tome, tabela istinitosti implikacije "Ako je A, onda B" ima oblik (vidi Dodatak 2 na slici 4).

Od dva iskaza A i B možete sastaviti novu izjavu, koja glasi ovako: "A ako i samo ako B". Ova izreka se zove ekvivalentne izjave A i B i označavaju: A B. Smatra se da je izjava A B istinita ako su oba iskaza A i B tačna ili su oba iskaza A i B netačna. U drugim slučajevima (tj. ako je jedan iskaz tačan, a drugi netačan), ekvivalent se smatra netačnim. Dakle, tabela istinitosti za ekvivalentnost A i B ima oblik (vidi Dodatak 2 na slici 5).

1.3 Logičko rezonovanje

Svako rezonovanje se sastoji od lanca izjava koje proizlaze jedna iz druge prema određenim pravilima. Sposobnost rasuđivanja, ispravnog potkrepljivanja svojih zaključaka neophodna je ljudima bilo koje profesije. Čovek uči da rasuđuje od trenutka kada počne da govori, ali svrsishodno učenje logike rasuđivanja počinje u školi. Već osnovni predmet matematike podrazumijeva razvijanje sposobnosti učenika u poređenju, klasificiranju objekata, analiziranju činjenica, dokazivanju najjednostavnijih tvrdnji. Dosljednost rasuđivanja potrebna je ne samo za rješavanje matematičkih problema, već i za gramatičku analizu, savladavanje principa prirodne istorije itd. Dakle, nastavnik osnovne škole mora biti upoznat sa logikom, tj. sa naukom o zakonima i oblicima mišljenja, o opštim shemama rasuđivanja.

Glavne vrste sudova i zaključaka razmatraju se u klasičnoj logici koju je stvorio starogrčki filozof Aristotel (384-322 pne).

U logici se rasuđivanje dijeli na:

1. ispravan;

2. netačno.

Ispravno rasuđivanje je rasuđivanje u kojem se poštuju sva pravila i zakoni logike. Pogrešno zaključivanje je rasuđivanje u kojem se prave logičke greške zbog kršenja pravila ili zakona logike.

Logičke greške su dvije vrste:

1.paralogizmi;

2. sofizmi.

Paralogizmi su logičke greške koje nastaju u procesu zaključivanja nenamjerno (nesvjesno).

Sofizmi su logičke greške koje se namjerno prave u procesu rasuđivanja s ciljem da se zavede protivnik, opravda lažni iskaz, kakve gluposti itd.

Sofizmi su poznati od davnina. Takva razmatranja su sofisti naširoko koristili u svojoj praksi. Od njih potiče naziv "sofizam". Brojni primjeri rasuđivanja koje su sofisti koristili u raznim sporovima došli su do našeg vremena. Evo nekih od njih.

Najpoznatiji antički sofizam je rezon pod nazivom "Rogati".

Zamislite situaciju: jedna osoba želi uvjeriti drugu da ima rogove. Za to se daje sljedeće opravdanje: „Ono što nisi izgubio, imaš. Nisi izgubio rog. Dakle, imaš rogove."

Na prvi pogled, ovo razmišljanje izgleda ispravno. Ali u njemu je napravljena logička greška, koju osoba koja ne razumije logiku teško da će moći odmah pronaći.

Dajemo još jedan primjer. U Protagori (osnivač škole sofista) bio je Evatlov učenik. Nastavnik i učenik sklopili su dogovor prema kojem će Evatl plaćati školarinu tek nakon što dobije svoju prvu parnicu. Ali nakon što je završio studije, Evatl nije žurio da govori na sudu. Učiteljevo strpljenje je ponestalo, pa je podnio tužbu protiv svog učenika "Evatl će mi u svakom slučaju morati platiti", pomisli Protagora. - On će ili dobiti ovaj proces, ili ga izgubiti. Ako pobedi - plati po dogovoru; ako izgubi, platiće po presudi suda." „Ništa od toga“, tvrdio je Evatl. - Zaista, ili ću dobiti proces ili ga izgubiti.

Ako dobijem, odluka suda će me osloboditi plaćanja, ali ako izgubim, neću platiti prema našem dogovoru *.

Ovaj primjer također dozvoljava logičku grešku. A koji - saznaćemo dalje.

Glavni zadatak logike je analizirati ispravna razmatranja. Logičari nastoje da identifikuju i istraže obrasce takvih razmatranja, da definišu njihove različite vrste, itd. Neispravno zaključivanje u logici analizira se samo sa stanovišta grešaka koje su u njima napravljene.

Treba napomenuti da ispravnost obrazloženja ne znači istinitost njegovih premisa i zaključaka. Općenito, logika se ne bavi utvrđivanjem istinitosti ili lažnosti premisa i zaključaka razmatranja. Ali u logici postoji takvo pravilo: ako su razmatranja pravilno izgrađena (u skladu s pravilima i zakonima logike) i istovremeno se zasnivaju na istinitim premisama, onda će zaključak takvog rasuđivanja uvijek biti bezuvjetno istinit. U drugim slučajevima, istinitost rezultata se ne može garantovati.

Dakle, ako su razmatranja pogrešno konstruirana, onda, čak i uprkos činjenici da su njegove premise tačne, zaključak takvog rasuđivanja može biti istinit u jednom slučaju, a lažan u drugom.

Razmotrite, na primjer, ova dva razmatranja, koja su izgrađena prema istoj pogrešnoj shemi:

(1) Logika je nauka.

Alhemija nije logika.

Alhemija nije nauka.

(2) Logika je nauka.

Zakon nije logika.

Pravo nije nauka.

Očigledno, u prvom argumentu zaključak je tačan, ali u drugom je netačan, iako su premise u oba slučaja istinite tvrdnje.

Takođe je nemoguće garantovati istinitost zaključka razmatranja kada je barem jedna od njegovih premisa netačna, čak i ako je ovo rezonovanje ispravno.

Ispravno rasuđivanje je rasuđivanje u kojem neke misli (zaključci) nužno slijede iz drugih mišljenja (premisa).

Primjer ispravnog rezonovanja može biti sljedeći zaključak: „Svaki građanin Ukrajine mora priznati svoj Ustav. Svi narodni poslanici Ukrajine su državljani Ukrajine. Dakle, svako od njih mora priznati Ustav svoje države", a primjer prave misli je presuda: "Postoje građani Ukrajine koji ne priznaju barem neke članove Ustava svoje države."

Sljedeće obrazloženje treba smatrati netačnim: „Pošto ekonomska kriza u Ukrajini se to očito osjeća nakon proglašenja nezavisnosti, potonje je razlog ove krize." Logička greška ovog tipa naziva se "nakon ovoga - zbog ovoga". Ona leži u činjenici da se vremenski slijed događaja u takvim slučajevima poistovjećuje s kauzalnim. Primjer neistinitog mišljenja može biti svaki stav koji ne odgovara stvarnosti, recimo, izjava da ukrajinska nacija uopće ne postoji.

Svrha spoznaje je sticanje istinskog znanja. Da biste uz pomoć rasuđivanja stekli takvo znanje, morate, prvo, imati prave preduslove, a drugo, pravilno ih kombinovati, rasuđivati ​​po zakonima logike. Koristeći lažne premise, prave činjenične greške, a kada krše zakone logike, pravila za konstruisanje razmatranja, prave logičke greške. Činjenične greške se, naravno, moraju izbjegavati, što nije uvijek moguće. Što se tiče logičkih, osoba visoke intelektualne kulture može izbjeći ove greške, jer su osnovni zakoni logički ispravnog mišljenja, pravila za građenje rasuđivanja, pa čak i smislena tipične greške u rasuđivanju.

Logika uči ispravno zaključivati, ne praviti logičke greške, razlikovati ispravno zaključivanje od pogrešnog. Ona klasifikuje ispravna razmatranja u svrhu njihovog sistemskog razumevanja. U tom kontekstu može se postaviti pitanje: budući da postoji mnogo razmatranja, da li je moguće, prema riječima Kozme Prutkova, obuhvatiti neograničeno? Da, možete, budući da vas logika uči rasuđivanju, fokusirajući se ne na konkretan sadržaj misli koje su dio rasuđivanja, već na shemu, strukturu rasuđivanja, oblik kombiniranja ovih misli. Recimo oblik rezonovanja poput “Svako x je y, a dati z je x; shodno tome, dato z" je tačno, a saznanje o njegovoj ispravnosti uključuje mnogo bogatije informacije od znanja o ispravnosti zasebnog materijalnog rezonovanja sličnog oblika. A oblik rezonovanja prema šemi „Svaki x je y, a z je takođe y; dakle, z je x "odnosi se na netačno. Kao što gramatika proučava oblike riječi i njihove kombinacije u rečenici, apstrahirajući od konkretnog sadržaja jezičkih izraza, tako i logika proučava oblike mišljenja i njihove kombinacije, apstrahirajući od konkretnog sadržaja tih misli.

Da bi se otkrio oblik misli ili razmatranja, potrebno ih je formalizirati.

Zaključci za 1. poglavlje

Na osnovu prethodno navedenog mogu se izvući sljedeći zaključci:

1. Logika se pojavila kao grana filozofskog znanja. Glavni razlozi za nastanak su razvoj nauke i govorništva. Budući da je nauka zasnovana na teorijskom mišljenju, koje pretpostavlja konstrukciju zaključaka i dokaza, postaje neophodno proučavati samo mišljenje kao oblik spoznaje.

2. U modernoj nauci značaj simboličke logike je veoma velik. Primjene pronalazi u kibernetici, neurofiziologiji, lingvistici. Simbolička logika je moderna faza u razvoju formalne logike. Proučava procese zaključivanja i dokazivanja putem njihovog prikaza u logičkim sistemima. Dakle, po svom predmetu ova nauka je logika, a po svom metodu matematika.

Proučivši materijale, razjasnili smo naše ideje o matematičkim konceptima:

Ovo su koncepti o idealnim objektima;

Svaki matematički koncept ima pojam, obim i sadržaj;

Definisani su koncepti; mogu biti eksplicitne ili implicitne. Implicitne definicije uključuju kontekstualne i ostenzivne definicije;

Proučavanje pojmova se odvija od razreda do razreda uz napredno proučavanje teme.

Proučavajući gradivo, upoznali smo se sa pojmovima uz pomoć kojih smo razjasnili značenje veznika "i", "ili" koji se koriste u matematici, čestica "ne", riječi "svako", "postoji", "dakle" i "ekvivalentno". Ovo su koncepti:

Izgovaranje;

Elementarne izjave;

Logički spojevi;

Složene izjave;

Povezivanje izjava;

Disjunkcija izjava;

Poricanje izjava.

Uzeti u obzir pravila:

Određivanje istinitosti složene izjave;

Konstruisanje negacije rečenica različite strukture.

Poglavlje 2. Upotreba elemenata matematičke logike u nastavi matematike u osnovnim razredima

2.1 Upotrebaelementi logike u osnovnom kursu matematike

Matematika daje stvarne preduslove za razvoj logičkog mišljenja, zadatak nastavnika je da te mogućnosti što bolje iskoristi prilikom podučavanja djece matematike. Međutim, poseban program za razvoj logičkih metoda mišljenja, koji treba formulisati u studiji ovu temu, ne Kao rezultat toga, rad na razvoju logičkog mišljenja se nastavlja bez poznavanja sistema potrebnih tehnika, bez poznavanja njihovog sadržaja i redoslijeda formiranja.

Barakina V.T. ističe sljedeće zahtjeve za znanjem, vještinama i sposobnostima učenika u izučavanju elemenata logike u osnovnoj školi:

1. Elementi teorije skupova:

Upoznati skupove različite prirode na konkretnim primjerima i načinima njihovog evidentiranja (nabrajanje);

Naučite da istaknete elemente seta;

Da se upoznaju sa glavnim tipovima relacija između skupova i načinom njihovog predstavljanja pomoću Euler-Vennovih krugova;

Naučite izvoditi neke operacije nad skupovima (unija, sjecište).

2. Elementi teorije iskaza:

Upoznati se sa izjavom na nivou reprezentacija;

Naučite razlikovati izjave od drugih rečenica;

Upoznajte se sa glavnim vrstama izjava;

Naučite izvoditi neke operacije nad iskazima (negacija, konjunkcija, disjunkcija).

3. Elementi kombinatorike:

Upoznajte se sa ovim konceptom na nivou reprezentacija;

Naučite razlikovati kombinatorne probleme od drugih vrsta riječnih zadataka koji se razmatraju na časovima matematike;

Naučite rješavati probleme za određivanje broja položaja od n elemenata po m elemenata.

Elementi logike u osnovnoj školi razmatraju se i na časovima matematike i informatike. Istovremeno, nivo zahtjeva za znanjem, sposobnostima i vještinama učenika, kao i sadržaj obuke u ovoj sekciji, donekle se razlikuju u različitim programima. Ovo je prvenstveno zbog činjenice da trenutno Federalni državni obrazovni standard osnovnog opšteg obrazovanja ne podrazumijeva obavezno razmatranje ove teme u razredima 1-4.

Trenutno su svi predmeti matematike usmjereni na razvoj učenika. Tako, na primjer, kurs Istomine N.B. njen glavni cilj je razvoj metoda misaone aktivnosti učenika, mentalnih operacija: analiza, sinteza, poređenje, klasifikacija, analogija, generalizacija.

Slični dokumenti

Studiranje kursa matematičke logike. Osnova logike je razumijevanje strukture matematičke nauke, njenih temeljnih koncepata. Istorijska skica... Ekvivalencija rečenica. Poricanje izjava. Logično praćenje.

teza, dodana 08.08.2007


Vannastavne aktivnosti kao jedan od oblika rada. Pedagoške osnove izučavanja matematičke logike u srednjoj školi u okviru vannastavnih aktivnosti. Analiza postojećih metoda za formiranje općih logičkih i logičkih vještina kod školaraca.

seminarski rad, dodan 19.11.2012


Osnove metoda za proučavanje matematičkih pojmova. Matematički pojmovi, njihov sadržaj i obim, klasifikacija pojmova. Psihološko-pedagoške karakteristike nastave matematike u 5-6 razredima. Psihološki aspekti formiranja pojmova.

teza, dodana 08.08.2007


Jezičke osnove učenja pridjeva u osnovnoj školi. Psihološko-pedagoške osnove proučavanja pridjeva u osnovnoj školi. Metode rada na pridevu po sistemu razvojnog obrazovanja L.V. Zankova.

teza, dodana 03.04.2007


Teorijske osnove pripreme djece za nastavu matematike u školi. Pitanja pripreme djece za školu u psihološko-pedagoškoj i metodičkoj literaturi. Pojam, suština, značenje matematičke spremnosti za učenje u školi. Istraživački program.

seminarski rad, dodan 23.10.2008


Osobine izučavanja matematike u osnovnoj školi prema Federalnom državnom obrazovnom standardu osnovnog opšteg obrazovanja. Sadržaj kursa. Analiza osnovnih matematičkih pojmova. Suština individualnog pristupa u didaktici.

seminarski rad dodan 29.09.2016


Psihološko-pedagoške osnove razvoja logičkog mišljenja kod mlađih učenika. Izrada metodologije za rješavanje problema formiranja logičke pismenosti učenika na časovima matematike u osnovnoj školi, primjeri rješavanja nestandardnih aritmetičkih zadataka.

disertacije, dodato 31.03.2012


Teorijske i metodološke osnove ispitne stavke i njegove vrste. Psihološke i pedagoške osnove. Testovi na časovima matematike. Analiza iskustva nastavnika u primeni test zadataka. kratak opis prednosti korištenja obrasca za kontrolu testa.

seminarski rad dodan 17.04.2017


Psihološke karakteristike mlađeg učenika. Tehnike i metode upotrebe elemenata etimološke analize u nastavi u osnovnoj školi. Karakteristike nastave pismenog pisanja za mlađe učenike. Analiza nastavnog materijala "Ruski jezik" u osnovnoj školi.

teze, dodato 24.03.2015


Razvoj govora učenika na časovima matematike. Tehnike razvoja matematičkog govora. Veze između govora, mišljenja i jezika. Razvoj konzistentnosti, ekspresivnosti, dokazanosti i tačnosti matematičkog govora. Podizanje nivoa govorne kulture učenika.

Da biste vidjeli ovaj formatirani i označeni PDF, preuzmite ga i otvorite na svom računalu.
Ministarstvo obrazovanja Orenburške oblasti

Državna autonomna stručna obrazovna ustanova
"Orsk Engineering College"

Orsk, oblast Orenburg

Istraživanja

matematike

«
MATEMATIKA BEZ
FORMULE, JEDNAČINE I
NEJEDNAKOSTI
»

Pripremljeno
:
Thorik Ekaterina
,

studentska grupa
15LP

Supervizor:
O.V.Marčenko
.,

kolega učitelj
matics

Matematika
–

ovo je poseban svijet u kojem formule igraju vodeću ulogu,
simboli i geometrijski objekti. U istraživanju str
šta smo odlučili
saznajte što se događa ako uklonite formule, jednadžbe i
nejednakost?

Relevantnost ove studije je u tome

iz godine u godinu
izgubljeno je interesovanje za matematiku. Ne vole matematiku, prvenstveno iz
-
za formule.
U ovom

Radom želimo ne samo pokazati ljepotu matematike, već i
prevladati ideje „suvoće“ koje se pojavljuju u glavama učenika,
formalni karakter, izolovanost ove nauke od života i prakse.

Svrha rada: dokazati da će matematika ostati potpuna
nauka, sa
ovo zanimljivo i višestruko, ako iz nje uklonimo formule, jednadžbe i
nejednakost.

Radni zadaci:
pokaži tog matematičara
a

bez formula, jednadžbi i
nejednakosti
je puna nauka
; sprovesti anketu
cipele
cha
NS
stidljiv; ispitati
informativni
e izvori; upoznati se sa glavnim načinima rješavanja
logičkih zadataka.

Pod pretpostavkom da su matematičke formule
-

samo udoban jezik
za prezentaciju ideja i metoda matematike, onda se te ideje mogu opisati,
koristeći poznate i vizuelne slike iz o
uskovitlanog života.

Predmet našeg istraživanja bili su načini rješavanja matematičkih
problemi bez formula, jednačina i nejednačina.

Studenti našeg koledža su zamoljeni da odgovore na pitanje: šta
postaće sa matematikom, ako iz nje izbaciš formule, jednačine i ne
jednakost?
odabirom jednog odgovora od sljedećih opcija:

a) ostat će brojevi, brojevi, slova b) ostat će samo teorija

c) ostaju teoreme i dokazi d) ostaju grafovi

e) matematika će postati književnost g) ništa neće ostati

Rezultati ovoga
anketa je pokazala da je većina učenika samouvjerena i bez
formule, jednačine i nejednačine, matematika će postati književnost. Odlučili smo
opovrgnuti ovo mišljenje. Bez formula, jednačina i nejednačina u matematici, u
prije svega, bit će logički zadaci koji
e najčešće čine
većinu zadataka na matematičkoj olimpijadi. Raznolikost logičkog
zadaci su veoma veliki. Postoji i mnogo načina za njihovo rješavanje. Ali najveći
Raširili su se: metoda zaključivanja, metoda tabela, metoda
broji, kruži hej
lera, blok metoda
-
sheme.

Način rasuđivanja

najprimitivniji način. Na ovaj način
rješavaju se najjednostavniji logički problemi. Njegova ideja je da mi
provodimo rasuđivanje koristeći sukcesivno sve uslove problema, i
dolazimo do zaključka da
će biti odgovor na problem.
Na ovaj način
obično rješavaju jednostavne logičke probleme.

Glavna tehnika koja se koristi pri rješavanju tekstualnih logičkih
zadaci je
građevinski stolovi
... Tablice ne dozvoljavaju samo vizualne
predstavljaju uslov
sretno ili njen odgovor, ali puno pomaže
donose ispravne logičke zaključke u toku rješavanja problema.

Metod grafa.
Graf
-

to je skup objekata sa vezama između njih.
Objekti su predstavljeni kao vrhovi, ili čvorovi grafa (označeni su
onda
chkami) i veze
-

poput lukova ili ivica. Ako je veza jednosmjerna
označeno na dijagramu linijama sa strelicama, ako je veza između objekata
dvostrano je na dijagramu označeno linijama bez strelica.

Metoda Eulerovih krugova.
Za rješavanje se koriste Ojlerovi dijagrami

velika grupa logičkih zadataka. Svi ovi zadaci se uslovno mogu podijeliti u tri
tip. U problemima prvog tipa potrebno je simbolički izraziti mnoge
gestovi,
osenčen u Ojlerovim dijagramima pomoću znakova
ki prelaze operacije,
asocijacije i dodaci.
U problemima drugog tipa, Ojlerov dijagram
koriste se za analizu situacija povezanih s definicijom klase. Treći tip
problemi u čijem rješavanju se koriste Ojlerovi dijagrami,
-

zadaci za
logički račun.

Blok metoda
-
sheme
.
Ovakvo logično rješavanje problema
uključeno u kurs
podučavanje studenata obrazovnih institucija na kursu informatike.
Programiranje jezika
Pascal
.

Pored logičkih problema u matematici, n
oroy riješiti jednostavno
matematičkih problema, morate raditi apsurdne stvari koje idu dalje
ra
tragove naše logike, našeg razmišljanja.
Apsurdno
–

u matematici i logici,
znači šta
-
tada element nema značenje unutar datog
teorija,

sistemi ili

polja, suštinski nekompatibilna s njima, iako element,
što je u ovom sistemu apsurdno
eme može imati smisla u drugom.

U matematici se sofizmi (vještina, vještina) izdvajaju u posebnu grupu.
-

složeno zaključivanje, koje ipak pri površnom ispitivanju
izgleda da je tačno.

Bez formula u matematici može nastati situacija kada
toraya can
postoji u stvarnosti, ali nema logično objašnjenje. Takva situacija
naziva paradoksom. Pojava paradoksa nije ništa
-
onda
nezakonito, neočekivano, slučajno u istoriji razvoja nauke
razmišljanje. Signalizirajući njihov izgled
govori o potrebi revizije prethodnog
teorijskih koncepata, unapređenje adekvatnijih koncepata, principa
i metode istraživanja.

Svijet nauke poput matematike nije ograničen samo na rješenje
posebne vrste zadataka. Pored svih poteškoća, u

ona ima nesto lepo i zanimljivo,
ponekad čak i smešno. Matematički humor, baš kao i svet matematike,
sofisticiran i poseban.

Dakle, bez formula, jednačina i nejednačina, matematika će ostati
puna nauka, istovremeno zanimljiva i višestruka.

Bibliografska lista.

Agafonova, I. G. Učenje razmišljanja: Zabavni logički problemi,
testovi i vježbe za djecu. Tutorial [Tex] /
I. G. Agafonova

SPb.
IKF MiM
–

ekspresno, 1996.
–

Balayan E.N. 1001 olimpijada i zabavni zadaci
i po
matematike
[Tex]

/ E.N. Balayan.
-

3
-
e ed.
-

Rostov n/a: Phoenix, 2008.
-

Farkov, A. V. Matematičke olimpijade u školi. 5
-
11 klasa.
[Tex] /

A. V. Farkov.
-

8
-
izd., rev. i dodati.
-

M.: Iris
-
štampa, 2009.
-

http://www.arhimedes.org/

Turnirirajte ih. M.V. Lomonosov (Moskva)
http://olympiads.mccme.ru/turlom/

Priloženi fajlovi

Metode rješavanja logičkih problema

Trosheva Natalia, 7 razred

1 . Svakom specijalistu je potrebna logika, bilo da je matematičar, ljekar ili biolog. Logika je potreban alat, oslobađajući od nepotrebnog, nepotrebnog pamćenja, pomažući da se u masi informacija pronađe ono vrijedno koje je osobi potrebno. Bez logike, ovo je rad na slijepo.

Tokom svih godina školovanja rješavamo mnoštvo raznih problema, uključujući i logičke: zadatke zabavnog karaktera, zagonetke, anagrame, rebuse itd. Da bi se uspješno rješavali problemi ove vrste, potrebno je biti u stanju identificirati njihove zajedničke karakteristike, uočiti obrasce, postaviti hipoteze, testirati ih, izgraditi lance rasuđivanja i izvući zaključke. Logički problemi se razlikuju od običnih po tome što ne zahtijevaju proračune, već se rješavaju rasuđivanjem. Možemo reći da je logički zadatak posebna informacija koju ne samo da treba obraditi u skladu sa datim uslovom, već se želi i uraditi. Posebno mjesto u matematici su zauzeti zadaci čije rješavanje razvija logičko mišljenje, što doprinosi uspješnom proučavanju predmeta. Ovi zadaci su zabavni i ne zahtijevaju puno matematičkog znanja, pa privlače i one učenike koji matematiku baš i ne vole.

2. Moj obrazovna istraživanja rad je teorijski.

Svrha rad je poznat različite vrste logičke probleme, algoritam i metode za njihovo rješavanje.

Za postizanje ovog cilja potrebno je riješiti sljedeće zadaci:

1. proučavati literaturu kako bi se upoznali sa različitim vrstama logičkih problema i metodama njihovog rješavanja,

2. primijeniti ove metode na rješavanje različitih vrsta logičkih problema, 3. odabrati logičke probleme koje treba riješiti određenom metodom.

Objekt istraživanja - logički zadaci u nastavnom planu i programu matematike u obrazovnoj školi.

Stavka istraživanja - razne metode za rješavanje logičkih problema.

Metode istraživanje:

analiza i sinteza, poređenje.

3. Rješenje mnogih logičkih problema povezano je s razmatranjem nekoliko konačnih skupova sa istim brojem elemenata, između kojih je potrebno uspostaviti korespondenciju. Prilikom rješavanja takvih problema pogodan je za korištenje algoritam rješenja

Prilikom rješavanja logičkih zadataka koristimo sljedeće algoritam:

1) Određivanje sadržaja teksta (izbor objekata ili subjekata).

2) Prikupljanje potpunih informacija o događaju koji se dogodio.

3) Formiranje problema isključivanjem dijela informacije ili njenom iskrivljavanjem.

4) Proizvoljna formulacija problema. Ako je potrebno (nedostatak informacija, izobličenje, itd.), uvodi se dodatni logički uslov.

5) Provjera mogućnosti rješenja pomoću rasuđivanja. Primanje jedinog doslednog odgovora znači da je uslov sastavljen, istina je. Ako nije, pogledajte dodatnu klauzulu 6.

6) U pripremljenom stanju nedostaju informacije ili su dostupne informacije kontradiktorno iskrivljene. Mijenjamo ili dopunjujemo stanje zadatka, nakon čega je potrebno pogledati tačku 5.

4. Za razvoj pamćenja, generalizaciju stečenog znanja, zanimljivi su logički testovi. Za rješavanje matematičkih testova, pored znanja iz školske matematike, potrebno je promatrati, upoređivati, generalizirati, izvoditi analogije, izvoditi zaključke i opravdavati ih. U osnovi, testovi su zadaci kreativne prirode koji doprinose razvoju logičkog mišljenja.

Logički testovi su klasifikovani u tri glavne grupe:

verbalno

simboličko-grafičko

kombinovano

Svijet simboličko-grafičkih logičkih testova vrlo je raznolik i bogat. Zadaci su efikasan metod odnos algebarskog materijala sa slikom matematičkih figura.

Umetnite oblik koji želite:

? 100

Primjer. Unesite riječ koja nedostaje

matematika 3≤x≤6 tema

decimetar 5≤x≤8?

Logika pomaže da se znanje usvoji svesno, sa razumevanjem, tj. nije formalno; stvara priliku za bolje međusobno razumijevanje. Logika je umjetnost rasuđivanja, sposobnost izvođenja ispravnih zaključaka. To nije uvijek lako, jer se vrlo često potrebne informacije „maskiraju“, iznose implicitno i mora se moći izvući.

5. Logički zadaci zasnovani na tekstu mogu se uslovno podeliti na sledeće tipove:

sve izjave su istinite;

nisu sve izjave tačne;

problemi o ljubiteljima istine i lažovima.

Savjetuje se rješavanje svake vrste problema postepeno, u fazama.

6. Razmotrimo glavne metode rješavanja problema i primjenu nekih metoda na određene probleme.

Metoda rasuđivanja

U metodi zaključivanja, pri rješavanju, pomažu: dijagrami, crteži, kratke bilješke, mogućnost odabira informacija, sposobnost korištenja pravila nabrajanja.

Primjer.

Lena, Olya, Tanya su učestvovale u trci na 100 m. Lena je trčala 2 sekunde ranije od Olye, Olya je trčala 1 sekundu kasnije od Tanje. Ko je dotrčao ranije: Tanja ili Lena i na koliko sekundi?

Rješenje.

Napravimo dijagram:

Lena __________

Olya __________ __ __

Tanya __________ __

Odgovori. Prethodno je Lena došla do 1s.

Metoda opisivanja objekata i njihovih oblika

Iz opisa možete zamisliti objekt, mjesto ili događaj koji nikada niste vidjeli. Prema znakovima (atributima) zločinca, oni čine njegov navodni portret - kompozitnu skicu.

Prema znacima (simptomima) bolesti lekar postavlja dijagnozu, tj. prepozna bolest.

Rešavanje mnogih zagonetki, šarada, rešavanje ukrštenih reči zasniva se na prepoznavanju predmeta iz njegovog opisa.

Metoda traženja povezanih zadataka

Ako je problem težak, onda je potrebno pokušati pronaći i riješiti jednostavniji "srodni" problem. Ovo daje ključ za rješavanje prvobitnog problema.

Metoda "pročešljavanja zadataka" (ili "možete pretpostaviti da...")

Problem možete riješiti po potrebi ili ga prvo možete transformirati u oblik koji je prikladan za njegovo rješavanje: preformulirajte uvjet na pogodnijem jeziku (na primjer, na jeziku crteža), odbacite jednostavne slučajeve, smanjite opći slučaj na određenu.

Metoda par-nepar

Mnogi problemi se mogu lako riješiti ako primijetite da određena vrijednost ima određeni paritet. Iz ovoga slijedi da su situacije u kojima data vrijednost ima drugačiji paritet nemoguće. Ponekad se ova vrijednost mora "konstruirati", na primjer, da se uzme u obzir paritet sume ili proizvoda, da se razbiju objekti u parove. Uočite izmjenu stanja, bojite objekte u dvije boje, itd.

Primjeri.

Skakavac je skočio duž prave linije i vratio se na početnu tačku (dužina skoka 1m). Dokažite da je napravio paran broj skokova.

Rješenje. Pošto se skakavac vratio na svoju početnu tačku. Broj skokova udesno jednak je broju skokova ulijevo, tako da je ukupan broj skokova paran.

"Obrnuti" metod

Ako je neka operacija navedena u problemu, a ona je reverzibilna, tada možete napraviti "obrnuti" pomak od konačnog rezultata do originalnih podataka. (Na primjer, treba da iznesete ormarić iz sobe. Hoće li proći kroz vrata? Hoće, jer je unet kroz vrata). Analiza s kraja na kraj koristi se za pronalaženje pobjedničkih i poraženih situacija.

Table Method

Ova metoda se sastoji u sastavljanju tabele i unosu podataka u nju prema stanju problema

Metod grafa

Riječ "graf" pojavila se u matematičkoj literaturi sasvim nedavno. Koncept grafa koristi se ne samo u matematici, već iu tehnologiji, pa čak iu svakodnevnom životu pod raznim nazivima - dijagram, dijagram.

Grafovi su posebno korisni u rješavanju logičkih problema. Predstavljajući objekte koji se proučavaju u vizuelnom obliku, „grafovi“ pomažu da se zadrže u pamćenju brojne činjenice sadržane u iskazu problema, da se uspostavi veza između njih.

Count naziva se bilo koji skup tačaka, od kojih su neke povezane linijama ili strelicama. Pozivaju se tačke koje predstavljaju elemente skupa vrhovi graf, koji povezuje njihove segmente - rebra graf. Presječne točke ivica grafa nisu njegovi vrhovi. Da bi se izbjegla zabuna, vrhovi grafa se često ne prikazuju kao tačke, već u malim krugovima. Ponekad je prikladnije prikazati rubove ne ravnim segmentima, već lukovima.

Metoda Eulerovih krugova

Ovaj metod daje još vizuelniji prikaz mogućeg načina prikazivanja uslova, zavisnosti, odnosa u logičkim problemima.

Jedan od najvećih matematičara, akademik iz Sankt Peterburga Leonard Euler, napisao je više od 850 naučni radovi... Ovi krugovi su se pojavili u jednom od njih. Ojler je tada napisao da su "veoma pogodni za olakšanje našeg razmišljanja". Uz krugove, u takvim se zadacima koriste pravokutnici i drugi oblici.

Primjer.

1. Neki stanovnici grada govore samo ruski, neki samo uzbečki, a neki oba jezika. 85% govori uzbečki, 75% govori ruski. Koliko posto stanovnika govori oba jezika?

Rješenje. Hajde da napravimo šemu -

U krugu ispod slova "U" označit ćemo stanovnike koji govore uzbečki, ispod slova "R" - na ruskom. U zajedničkom dijelu krugova odredit ćemo stanovnike koji govore oba jezika. Sada od svih stanovnika (100%) oduzimamo krug "U" (85%), dobijamo stanovnike koji govore samo ruski (15%). A sada, oduzmimo ovih 15% od svih koji govore ruski (75%). Dobijamo govornike oba jezika (60%).

Kombinovana metoda

Metoda u kojoj se problem može riješiti na nekoliko načina.

Predloženi materijal "Metode rješavanja logičkih zadataka" može se koristiti kako u nastavi matematike, tako iu vannastavnim aktivnostima za učenike 5-9 razreda, nastavnike u cilju pripreme učenika za rješavanje olimpijskih zadataka, intelektualna takmičenja "Maraton znanja", regionalno takmičenje "Kengur"...

Upoznavši različite vrste logičkih problema i metode njihovog rješavanja, vjerujem da mogu primijeniti stečeno znanje u svojim obrazovnim aktivnostima, samostalno odabrati jednu ili drugu metodu rješavanja određenog problema, primijeniti proučavane metode na rješavanje problema u realna situacija.

Opštinska budžetska obrazovna ustanova

"Multidisciplinarni licej" gradskog naselja "Radničko naselje Chegdomyn" opštine Verkhnebureinsky

okruga Habarovskog kraja.

Apstraktni istraživački rad iz matematike:

Tema: "Metoda matematičke indukcije"

Završila: Antonova Svetlana

učenik 11 "B" razreda

Rukovodilac: O. A. Terentjeva

nastavnik matematike

grad Chegdomyn

1. Uvod 3

2. Istorija porekla

metoda matematičke indukcije 4-5

3. Ključni nalazi studije 6-14

4. Predviđeni zadaci za ispit 15-18

5. Zaključak 19 6. Literatura 20

Uvod:

Početkom 10. razreda počeli smo da učimo metodu matematičke indukcije, već tada me je ova tema jako zanimala, ali samo za učenje. Kada smo započeli intenzivnu pripremu za polaganje ispita iz matematike, zadaci na ovu temu su mi bili vrlo laki i zanimale su me mogućnosti ove metode pri rješavanju složenijih zadataka. Zajedno sa nastavnikom odlučili smo da detaljnije i temeljnije proučimo ovu metodu i njene mogućnosti prilikom rada na projektu na ovu temu.

Svrha mog rada:

Upoznati se sa metodom matematičke indukcije, sistematizovati znanja o ovoj temi i primeniti ovu metodu u rešavanju matematičkih zadataka i dokazivanju teorema.

Radni zadaci:

1. Aktuelizacija praktičnog značaja matematičkog znanja.

2. Razvoj moralnih ideja o prirodi matematike, suštini i porijeklu matematičke apstrakcije.

3. Ovladavanje različitim metodama i tehnikama rada.

4. Generalizacija i sistematizacija znanja o ovoj temi.

5. Primena stečenog znanja u rešavanju ispitnih zadataka.

problem:

Pokazati praktični značaj metode matematičke indukcije.

Iz istorije nastanka metode matematičke indukcije:

Izuzetna ekspanzija predmeta matematika u 19. veku privukla je sve veću pažnju na pitanja njegove „potkrijepljenosti“, tj. kritičku reviziju njenih polaznih tačaka (aksioma), izgradnju rigoroznog sistema definicija i dokaza, kao i kritičko ispitivanje logičkih primera koji se koriste u ovim dokazima.

Tek krajem 19. vijeka postojao je standard zahtjeva za logičkom strogošću, koji je do danas ostao dominantan u praktičnom radu matematičara na razvoju pojedinačnih matematičkih teorija.

Moderna matematička logika je dala definitivan odgovor na ovo pitanje: nijedna unificirana deduktivna teorija ne može iscrpiti razne probleme u teoriji brojeva.

Riječ indukcija na ruskom znači vođenje, a induktivnim se nazivaju zaključci doneseni na osnovu zapažanja, eksperimenata, tj. dobijen zaključkom od posebnog do opšteg.

Sva matematička istraživanja temelje se na deduktivnim i induktivnim metodama. Deduktivna metoda zaključivanja je rasuđivanje od opšteg ka posebnom, tj. rasuđivanje, čija je polazna tačka opšti rezultat, a konačna tačka je konkretan rezultat. Indukcija se koristi pri prelasku sa pojedinačnih rezultata na opšte, tj. je suprotnost deduktivnoj metodi.

Metoda matematičke indukcije može se uporediti sa napretkom. Počinjemo od najnižeg, kao rezultat logičkog razmišljanja dolazimo do najvišeg. Čovjek je oduvijek težio napretku, sposobnosti da logički razvija svoju misao, što znači da mu je sama priroda namijenila da razmišlja induktivno.

Uloga induktivnih zaključaka u eksperimentalnim naukama je veoma velika. Oni daju te propozicije, iz kojih se potom donose daljnji zaključci pomoću dedukcije. I iako se teorijska mehanika zasniva na tri Newtonova zakona kretanja, ovi zakoni su bili rezultat dubokog promišljanja eksperimentalnih podataka, posebno Keplerovih zakona o kretanju planeta, koje je izveo iz dugoročnih zapažanja danskog astronoma Tychoa. Brahe. Pokazalo se da su posmatranje i indukcija korisni u budućnosti za razjašnjavanje napravljenih pretpostavki. Nakon Michelsonovih eksperimenata o mjerenju brzine svjetlosti u pokretnom mediju, pokazalo se da je potrebno razjasniti zakone fizike, stvoriti teoriju relativnosti.

U matematici, uloga indukcije je u velikoj mjeri posljedica činjenice da ona leži u osnovi odabrane aksiomatike. Nakon što je duga praksa pokazala da je ravna putanja uvijek kraća od zakrivljene ili izlomljene putanje, bilo je prirodno formulirati aksiom: za bilo koje tri točke A, B i C, nejednakost

Koncept "praćenja..." temeljne aritmetike pojavio se i kada se posmatra formiranje vojnika, brodova i drugih uređenih skupova.

Međutim, ne treba misliti da se time iscrpljuje uloga indukcije u matematici. Naravno, ne bismo trebali eksperimentalno provjeravati teoreme koje su logički izvedene iz aksioma: ako u izvođenju nisu napravljene nikakve logičke greške, onda su istinite u onoj mjeri u kojoj su aksiomi koje smo prihvatili istiniti. Ali mnogo izjava može se izvesti iz ovog sistema aksioma. A izbor tih tvrdnji koje treba dokazati ponovo je podstaknut indukcijom. Ona vam omogućava da odvojite korisne teoreme od beskorisnih, ukazuje na to koje se teoreme mogu pokazati istinitima, pa čak i pomaže da se ocrta put dokaza.

U matematici se dugo koristi induktivna metoda, zasnovana na činjenici da se određena opšta tvrdnja daje na osnovu razmatranja samo nekoliko posebnih slučajeva. Istorija je, na primjer, sačuvala sljedeću Eilerovu izjavu: „Nemam drugih argumenata za dokaz, osim duge indukcije, koju sam do sada proveo da ni na koji način ne mogu sumnjati u zakon koji reguliše formiranje ovih članova. ... I čini se nemogućim da se zakon za koji je utvrđeno da je istinit, na primjer, za 20 članova, ne bi mogao biti poštovan za sljedeće."

Vjerujući u nepogrešivost indukcije, naučnici su ponekad pravili velike greške.

Do sredine sedamnaestog veka u matematici su se nakupili mnogi pogrešni zaključci. Počela se snažno osjećati potreba za znanstveno utemeljenom metodom koja bi omogućila izvođenje općih zaključaka na osnovu razmatranja nekoliko posebnih slučajeva. I takva metoda je razvijena. Glavne zasluge u tome imaju francuski matematičari Pascal (1623-1662) i Descartes, kao i švajcarski matematičar Jacob Bernoulli (1654-1705).

Glavni rezultati faze istraživanja.

U procesu rada saznao sam da se sve izjave mogu podijeliti na opšte i privatne. Primjer opće tvrdnje je, na primjer, tvrdnja: "U bilo kojem trokutu, zbir dviju stranica je veći od treće strane." Na primjer, izjava: "Broj 136 je djeljiv sa 2" je privatna.

Prelazak sa opštih iskaza na privatne se zove zaključiti cije. U matematici koristimo deduktivnu metodu, na primjer, u rasuđivanju ovog tipa: data figura je pravougaonik; za svaki pravougaonik dijagonale su jednake, dakle, za ovaj pravougaonik, dijagonale su jednake.

Ali uz to, u matematici je često potrebno prijeći sa pojedinačnih iskaza na opšte, tj. koristiti suprotnu deduktivnu metodu, koja se zove indukcija .

Induktivna pristup obično počinje analizom i poređenjem, posmatranjem ili eksperimentom. Ponavljanje neke činjenice vodi induktivnoj generalizaciji. Rezultat dobiven indukcijom, općenito govoreći, nije logički potkrijepljen niti dokazan. Mnogo je poznatih slučajeva kada su iskazi dobijeni indukcijom bili netačni. Odnosno, indukcija može dovesti do ispravnih i netačnih zaključaka.

Razmislite primjer... Zamena u kvadratni trinom P(x) = x 2 + x + 41 umjesto NS prirodni brojevi 1,2,3,4,5, nalazimo: P (1) = 43; P (2) = 47; P (3) = 53; P (4) = 61; P (5) = 71. Sve vrijednosti ovog trinoma su prosti brojevi. Zamjena umjesto NS brojevi 0, -1, -2, -3, -4, dobijamo: P (0) = 41; P (-1) = 41; P (-2) = 43; P (-3) = 47; P (-4) = 53. Vrijednosti ovog trinoma na navedenim vrijednostima varijable NS su takođe prosti brojevi. Pojavljuje se hipoteza da je vrijednost trinoma P (x) je prost broj za bilo koju cjelobrojnu vrijednost NS... Ali izraženo hipoteza je pogrešna, budući da je npr. P (41) = 41 2 +41+41=41∙43.

Budući da se kod ove metode zaključak donosi nakon raščlanjivanja nekoliko primjera koji ne pokrivaju sve moguće slučajeve, ova metoda se zove nepotpuna ili nesavršena indukcija.

Metoda nepotpune indukcije, kao što vidimo, ne dovodi do potpuno pouzdanih zaključaka, ali je korisna jer omogućava vam da formulišete hipotezu, što se onda može dokazati egzaktnim matematičkim rasuđivanjem ili opovrgnuti. Drugim riječima, nepotpuna indukcija u matematici se ne smatra legitimnom metodom rigoroznog dokaza, već je moćanheuristički metod otkrivanja novih istina.

Ako se zaključak donese na osnovu analize svih slučajeva, onda se takva metoda zaključivanja naziva puna indukcija.

Evo primjer slično rezonovanje. Neka je potrebno utvrditi da je svaki prirodan paran broj NS u roku od 10 NS Za to uzimamo sve takve brojeve i ispisujemo odgovarajuća proširenja: 10=7+3; 12=7+5; 14=7+7; 16=11+5; 18=13+5; 20=13+7 ... Ovih šest jednakosti pokazuje da je svaki od brojeva koji nas zanimaju zaista predstavljen kao zbir dva jednostavna člana.

Neka je određena izjava tačna u nekoliko posebnih slučajeva. Razmatranje svih ostalih slučajeva je ili potpuno nemoguće ili zahtijeva veliki broj proračuna. Kako znate da li je ova izjava uopšte tačna? Ovaj problem se ponekad može riješiti prijavom posebna metoda rezonovanje zove metoda matematičke indukcija .Na osnovu ovoga metoda laži princip matematička indukcija .

Ako pogađate ovisno o prirodnom brojun, zaistazan=1 i iz činjenice da je istina zan= k(gdek-bilo koji prirodnibroj), proizilazi da to važi i za sljedeći brojn= k+1, onda je pretpostavka tačna za bilo kojeprirodni brojn.

Metoda matematičke indukcije je efikasna metoda dokazivanja hipoteza (tvrdnji) zasnovana na primjeni principa matematičke indukcije, stoga vodi samo do ispravnih zaključaka.

Metodom matematičke indukcije ne mogu se svi zadaci riješiti, ali samo zadaci, parametrizirano neka varijabla. Ova varijabla se zove indukciona varijabla.

Metoda matematičke indukcije ima najveću primjenu u aritmetici, algebri i teoriji brojeva.

Primjer 1... Pronađite iznos Sn =

Prvo, nalazimo zbrojeve jednog, dva i tri člana. Imamo:

S 1 = ; S 2 = ; S 3 = .

U svakom od ovih slučajeva dobije se razlomak u čijem brojniku je broj članova, a u nazivniku broj, jedan veći od broja članova. Ovo vam omogućava da izrazite hipoteza ( pretpostavka) da za bilo koju prirodnu NS Sp =.

Za provjeru ove hipoteze koristit ćemo se metodom matematičke indukcije.

1) Kada NS = 1 hipoteza je tačna, pošto S 1 = .

2) Pretpostavimo da je hipoteza tačna za NS= k, tj

S k = .

Dokažimo da tada hipoteza mora biti tačna za NS = k+ 1, tj

S k +1 = .

stvarno, S k +1 = S k

S k +1 =

Dakle, na osnovu pretpostavke da je hipoteza S NS =

istina za n = k, dokazali smo da je i za NS = k + 1.

Stoga formula S NS = istina za sve prirodne NS.

Primjer 2. Dokažite to za bilo koji prirodan broj NS i bilo koji realni broj a -1 nejednakost tzv Bernoullijeva nejednakost (nazvan po švajcarskom matematičaru iz 17. veka Jacobu Bernoulliju) : (1+ a) NS ≥ 1 + ap.

1) Ako n = 1, onda je očito da je tačna nejednakost: (1 + a) 1 ≥ 1 + a.

2) Pretpostavimo da je nejednakost tačna za n= k: (1+ a) k ≥ 1 + ak.

Pomnožite obje strane posljednje nejednakosti pozitivnim brojem 1+ a, rezultirajući (1+ a) k +1 ≥ 1+ ak+ a+ a 2 k.

Odbacivanjem posljednjeg člana na desnoj strani nejednakosti, smanjujemo desnu stranu ove nejednakosti, pa stoga (1+ a) k +1 ≥ a(k+1).

Dobijeni rezultat pokazuje da nejednakost vrijedi i za n= k+1.

Oba dijela dokaza izvedena su metodom matematičke indukcije, pa stoga nejednakost vrijedi za bilo koji prirodan broj NS.

Imajte na umu da je cijelo rješenje podijeljeno na četiri faze:

1.baza(pokazujemo da je tvrdnja koja se dokazuje istinita za neke od najjednostavnijih specijalnih slučajeva ( NS = 1);

2.supozicija(pretpostavljamo da je tvrdnja dokazana za prvu To slučajevi; 3 .korak(pod ovom pretpostavkom, dokazujemo tvrdnju za slučaj NS = To + 1 ); 4. zaključak (na izjava je tačna za sve slučajeve, odnosno za sve NS) .

Druga verzija metode matematičke indukcije.

Neke tvrdnje nisu tačne za sve prirodne NS, ali samo za prirodne NS, počevši od nekog broja R. Ponekad je moguće dokazati takve tvrdnje metodom koja je nešto drugačija od gore opisane, ali joj je prilično slična. Sastoji se od sljedećeg.

Tvrdnja je tačna za sve prirodne vrijednosti.n ≥ p ako: 1) to je tačno za NS= p (a ne za NS= 1, kao što je gore pomenuto);

2) od važenja ove izjave za NS= k, gde je k ≥ p (a ne k ≥ 1, kao što je gore pomenuto), sledi da je takođe tačno za NS= k + 1.

Primjer 1... Dokažite da je za bilo koju jednakost

Proizvod na lijevoj strani jednakosti označavamo sa, tj.

to moramo dokazati.

Za n = 1 formula nije tačna (1 - 1) = 1 (netačno).

1) Provjerimo da li je ova formula tačna za n = 2. - istina.

2) Neka je formula tačna za n = k, tj.

3) Dokažimo da je ovaj identitet istinit i za n = k + 1, tj.

Po principu matematičke indukcije, jednakost vrijedi za svaki prirodni broj.

Primjer 2. Dokazati da je 22n + 1 za bilo koji prirodan broj n3.

1) Za n = 3, nejednakost je tačna. 223 + 1.

2) Pretpostavimo da je 22k + 1 (k3).

3) Dokažimo da je 2 2 (k + 1) + 1.

Zaista, 2 = 222 (2k + 1) = (2k + 3) (2k - 1) 2k + 3, pošto je 2k - 10 za bilo koju prirodnu vrijednost k. Dakle, 22n + 1 za sve n3.

Napomena o metodi matematičke indukcije.

Dokaz matematičkom indukcijom sastoji se od dvije faze.

lthpozornici. Provjeravamo da li je izjava tačna za n = 1 (ili za n =R, za gore opisanu metodu).

2. faza Pretpostavljamo da je izjava tačna za n =k, i, polazeći od ovoga, dokazujemo da je to tačno i za NS = k+1.

Svaki od ovih koraka je važan na svoj način, s obzirom na primjer P(x) = x 2 + x + 41, vidjeli smo da izjava može biti istinita u brojnim posebnim slučajevima, ali ne općenito. Ovaj primjer nas uvjerava koliko je važna 2. faza dokazivanja metodom matematičke indukcije. Ako ga izostavite, možete doći do pogrešnog zaključka.

Međutim, ne treba misliti da je 1. faza manje važna od druge. Sada ću dati primjer da pokažem do kakvog se apsurdnog zaključka može doći ako izostavimo 1. fazu dokaza.

"Teorema a". Za bilo koje prirodno n, broj 2p +1 čak.

DokazatijeojeO. Neka je ova teorema tačna za n =k, to je broj 2 k + 1 čak. Dokažimo da je onda broj 2(k+1)+ 1 je takođe čak.

stvarno, 2(k+1)+1 = (2 k+1 )+2.

Po pretpostavci, broj 2 k +1 je paran, pa je stoga i njegov zbir sa parnim brojem 2 paran. Teorema je "dokazana".

Da nismo zaboravili da proverimo da li je naša "teorema" tačna za n = 1, ne bismo došli do takvog "rezultata".

Primjeri primjene metode matematičke indukcije na dokaz nejednakosti.

Primjer 1. Dokazati da je za bilo koji prirodan broj n1

.

Lijevu stranu nejednakosti označavamo sa.

Dakle, za n = 2, nejednakost je tačna.

Neka za neki k. Dokažimo to onda i. Imamo , .

Upoređujući i, imamo , tj. .

Za bilo koji prirodan broj k, desna strana posljednje jednakosti je pozitivna. Zbog toga . Ali, dakle, i.

Primjer 2. Pronađite grešku u zaključivanju.

Izjava. Za bilo koji prirodan broj n vrijedi nejednakost.

Dokaz.

Neka nejednakost vrijedi za n = k, gdje je k neki prirodni broj, tj.

Dokažimo da tada nejednakost vrijedi i za n = k + 1, tj.

Zaista, najmanje 2 za bilo koji prirodan broj k. Na lijevu stranu dodajmo nejednakost (1), a na desnu 2. Dobijamo valjanu nejednakost, odnosno. Tvrdnja je dokazana.

Primjer 4:

Dokazati nejednakost

Gdje su x 1, x 2,…., X 3 proizvoljni pozitivni brojevi.

Ova važna nejednakost između aritmetičke sredine i geometrijske sredine n brojeva je jednostavna posljedica odnosa dokazane u prethodnom primjeru. Zaista, neka su x 1, x 2, ..., x n proizvoljni pozitivni brojevi. Razmotrimo n brojeva

Očigledno, svi ovi brojevi su pozitivni i njihov proizvod je jednak jedan. Prema tome, kao što je dokazano u prethodnom primjeru, njihov zbir je veći ili jednak n, tj.

≥ n

štaviše, znak jednakosti se dešava ako i samo ako je x 1 = x 2 = ... = x n.

Nejednakost između aritmetičke sredine i geometrijske sredine n brojeva često je korisna u dokazivanju drugih nejednakosti, u pronalaženju najmanjih i najvećih vrijednosti funkcija.

Primjena metode matematičke indukcije na sumiranje redova.

Primjer 5. Prove Formula

, n je prirodan broj.

Za n = 1, obje strane jednakosti postaju jedna i, prema tome, prvi uvjet principa matematičke indukcije je zadovoljen.

Pretpostavimo da je formula tačna za n = k, tj.

.

Dodajte ovu jednakost objema stranama i transformirajte desnu stranu. Onda dobijamo

Dakle, pošto je formula tačna za n = k, sledi da je tačna i za n = k + 1. Ova izjava je tačna za bilo koju prirodnu vrijednost k. Dakle, i drugi uslov principa matematičke indukcije je takođe zadovoljen. Formula je dokazana.

Primjer 6. Dokaži to.

Metoda matematičke indukcije u rješavanju problema djeljivosti.

Koristeći metodu matematičke indukcije, mogu se dokazati različite tvrdnje o djeljivosti prirodnih brojeva.

Sljedeću tvrdnju je relativno lako dokazati. Hajde da pokažemo kako se to dobija metodom matematičke indukcije.

Primjer 7... AkonAko je prirodan broj, onda je broj paran.

Za n = 1 tačna je naša izjava: - paran broj. Pretpostavimo da je to paran broj. Pošto je 2k paran broj, onda je i paran. Dakle, paritet je dokazan za n = 1, paritet se izvodi iz parnosti, pa čak i za sve prirodne vrijednosti n.

Primjer 8. Dokažite da je rečenica tačna

A (n) = (5 je višekratnik broja 19), n je prirodan broj.

Tvrdnja A (1) = (više od 19) je tačna.

Pretpostavimo da je za neku vrijednost n = k

A (k) = (više od 19) je tačno. Od tada

Očigledno je i A (k + 1) tačno. Zaista, prvi član je djeljiv sa 19 zbog pretpostavke da je A (k) tačno; drugi član je također djeljiv sa 19, jer sadrži faktor 19. Oba uslova principa matematičke indukcije su zadovoljena, dakle, tvrdnja A (n) je tačna za sve vrijednosti n.

Dokaz o identitetu

Primjer 9... Dokažite to za bilo koji prirodni n pravedna jednakost

Q.E.D.

Primjer 10... Dokaži identitet

1) Provjerimo da li je ovaj identitet tačan za n = 1.

2) Neka je identitet istinit i za n = k, tj.

3) Dokažimo da je ovaj identitet istinit i za n = k + 1, tj.

M je zbir 2) i 3).

Metoda matematičke indukcije u rješavanju zadataka o geometrijskoj progresiji

Primjer 11. Dokažimo da je zajednički član geometrijske progresije jednak

a NS = a 1 ∙ q n-1 , metodom matematičke indukcije.

n = 1:

a 1 = a 1 ∙ q 0

a 1 = a 1 ∙ 1

lijeva strana = desna strana.

n =k:

a k = a 1 ∙ q k -1

n =k+1:

a k +1 = a 1 ∙ q k

dokaz:

a k +1 = a k ∙ q = a 1 ∙ q k -1 ∙ q = a 1 ∙ q k,

Q.E.D.

Oba uslova principa matematičke indukcije su zadovoljena, a samim tim i formula a n = a 1 ∙ q n -1 važi za bilo koji prirodan broj NS.

Reality Tasks

Primjer 12:

Dokažimo da je zbir unutrašnjih uglova konveksnog n-ugla π (n-2).

1. Minimalni broj uglova je tri. Pa počnimo
dokaz sa n = 3. To vidimo za trougao
formula daje π (3 ~ 2) = π Izjava za n = 3

fer.

2. Pretpostavimo da je formula
je tačno za n = k. Hajde da to dokažemo
to je tačno za bilo koju konveksnu
(k +1) -gon. Hajde da prekinemo

(k +1) -gon dijagonala

tako da dobijemo k-ugao i trougao (vidi sliku).

Pošto je formula tačna za trougao i k-ugao, dobijamo π (k - 2) + π = π (k -1).

Dobićemo isto ako u originalnu formulu zamenimo n = k + 1: π (k +1 - 2) = π (k -1).

Predloženi zadaci za ispit.

Primjer 1.

Dokažite to za bilo koji prirodni broj n 9 n + 1 - 8p - 9 višestruko od 16.

1) Provjerimo da li je ova izjava tačna za n = 1:

9 2 - 8 – 9 = 81- 8 – 9 = 64, 64 16.

At n = 1 izjava je tačna.

2) Pretpostavimo da je ova izjava tačna za n =k :

(9 k +1 - 8 k - 9) 16.

3) I, dokažimo da je ova izjava tačna za n =k+1 :

(9 k +2 – 8 (k+1) - 9) 16.

dokaz:

9 k +2 - 8(k+1) – 9 =9 k +1 ∙ 9 1 - 8 k – 8 – 9 = 9 k + 1 ∙ 9 - 8 k – 17 =

= 9(9 k +1 - 8 k - 9) + 64 k + 64 = 9(9 k +1 - 8 k - 9) +64(k+1)=

= 9(9 k +1 – 8 k - 9)+ 64(k+1).

Dakle: ( 9(9 k +1 - 8 k - 9) + 64(k-1)) 16.

Dakle, oba uslova principa matematičke indukcije su zadovoljena, pa je stoga 9 k +1 - 8p-9 višestruko od 16 za bilo koji prirodni NS.

Primjer 2.

NS ispunjen je uslov:

1 3 +2 3 +3 3 +… n 3 =.

S n = .

Provjerimo da li je ova formula tačna za n = 1:

Lijeva strana = 1 3 =1

Desna strana =

Formula je ispravna za n = 1.

n= k:

1 3 +2 3 +3 3 +… k 3 =.

S k =.

n =k+1:

1 3 +2 3 +3 3 +…+(k+1) 3 =.

S k +1 = .

dokaz:

S k +1 = S k +(k+1) 3

Dakle, ova formula je tačna u dva slučaja i dokazano je da je tačna za n= k+1 stoga je istinito za bilo koji prirodan broj NS.

Primjer 3.

Dokažite to za bilo koji prirodan broj NS ispunjen je uslov:

1 ∙ 2 ∙ 3 ​​+ 2 ∙ 3 ​​∙ 4 +… + n (n + 1) (n + 2) =.

.

1) Provjerimo da li je ova formula tačna za n = 1:

Lijeva strana = 1∙2∙3=6.

Desni dio = .

6 = 6; uslov je istinit za n = 1.

2) Pretpostavimo da je ova formula tačna za n= k:

1∙2∙3+2∙3∙4+…+ k(k+1)(k+2)=.

S k =.

3) I, hajde da dokažemo da je ova formula tačna za n= k+1:

1∙2∙3+2∙3∙4+…+(k+1)(k+2)(k+3)=.

S k +1 =.

dokaz:

Dakle, ovaj uslov je tačan u dva slučaja i dokazano je da je tačan za n= k+1, dakle vrijedi za bilo koji prirodan broj NS.

Primjer 4.

Dokaži da bilo koji prirodni NS pravedna jednakost

1) Kada n = 1 dobijamo tačnu jednakost

2) Postavljajući hipotezu indukcije, razmotrite zbir na lijevoj strani jednakosti za n= k+1;

3) Da biste dovršili dokaz, zabilježite to

Dakle, jednakost je tačna.

Primjer 5.

u avionu, NS prave, od kojih dve nisu paralelne i tri ne prolaze kroz tačku. Odredite na koliko dijelova ove prave dijele ravan.

Nakon što smo nacrtali potrebne crteže, možemo napisati sljedeću korespondenciju između broja NS linije koje zadovoljavaju uslov problema i broj a NS dijelovi u koje ove linije razbijaju ravan:

Sudeći po prvim članovima, redosled, a NS je takva da su razlike a 2 -a 1 , a 3 -a 2 , a 4 -a 3 ,… napravi aritmetičku progresiju. Ako se poslužimo već analiziranim primjerom, onda to možemo pretpostaviti NS prave koje zadovoljavaju uslov problema dele ravan na

dijelovi. Ovu formulu je lako provjeriti za prvih nekoliko vrijednosti. NS međutim, naravno, iz ovoga još ne proizlazi da daje odgovor na predloženi problem. Ova tvrdnja zahtijeva dodatni dokaz metodom matematičke indukcije.

Odstupajući od upravo obavljene "selekcije", to ćemo i dokazati NS prave (od kojih dvije nisu paralelne i tri ne prolaze kroz jednu tačku) dijele ravan na a NS dijelovi gdje a NS izračunato po formuli.

Očigledno, za n = 1 formula je tačna. Postavljanje hipoteze indukcije, razmotrite k+1 linije koje zadovoljavaju uslov problema. Odabir od njih na proizvoljan način k prave linije, možemo reći da dijele ravan na

dijelovi. Priložimo sada (k+1) th straight. Pošto nije paralelna ni sa jednom od prethodnih linija, presecaće sve k direktno. Budući da neće proći ni kroz jednu presečnu tačku prethodnih pravih linija, proći će duž k+1 komad na koji je ravan već podijeljen, a svaki od ovih komada će biti podijeljen na dva dijela, tj. bit će dodano više k+1 komada. Dakle, ukupan broj komada na koje je ravan podijeljen k+1 pravo, tamo

Ovim je dokaz završen.

Zaključak

Dakle, indukcija (od lat. Inductio - vođenje, motivacija) je jedan od oblika zaključivanja, metoda istraživanja, pomoću koje se, iz poznavanja pojedinačnih činjenica, dolazi do opštih odredbi. Indukcija može biti potpuna ili nepotpuna. Metoda nepotpune indukcije sastoji se u prijelazu na univerzalnu formulaciju nakon provjere istinitosti pojedinih formulacija za pojedinačne, ali ne sve, vrijednosti n. Primjenjujući punu indukciju, smatramo da imamo pravo proglasiti istinitost univerzalne formulacije samo kada smo uvjereni u njenu istinitost za svaku vrijednost n, bez izuzetka. Metoda matematičke indukcije je metoda dokazivanja zasnovana na principu matematičke indukcije. Omogućava, u potrazi za općim zakonom, da se testiraju hipoteze, odbace lažne i potvrđuju istinite.

Metoda matematičke indukcije je jedna od teorijskih osnova za rješavanje problema sumiranja, dokazivanje identiteta, dokazivanje i rješavanje nejednačina, rješavanje pitanja djeljivosti, pri proučavanju svojstava numeričkih nizova, pri rješavanju geometrijskih zadataka itd.

Upoznavajući se sa metodom matematičke indukcije, proučavao sam specijalnu literaturu, konsultovao se sa nastavnikom, analizirao podatke i rešenja problema, koristio internet resurse i izvršio potrebne proračune.

Izlaz:

U toku svog rada naučio sam da je za rješavanje zadataka metodom matematičke indukcije potrebno poznavati i razumjeti osnovni princip matematičke indukcije.

Prednost metode matematičke indukcije je njena svestranost, budući da se ovom metodom mogu riješiti mnogi problemi. Nedostatak nepotpune indukcije je što ponekad vodi do pogrešnih zaključaka.

Uopštivši i sistematizirajući znanja o matematičkoj indukciji, uvjerio sam se u potrebu znanja na temu "metoda matematičke indukcije". Osim toga, ovo znanje povećava interesovanje za matematiku kao nauku.

Takođe, u toku rada stekao sam veštine rešavanja zadataka metodom matematičke indukcije. Vjerujem da će mi ove vještine pomoći u budućnosti.

Bibliografija.

1. Bokovnev O. A., Firsov V. V., Shvartsburd S. I. Odabrana pitanja matematike. 9. razred. Izborni predmet.-M.: Obrazovanje, 1979.

2. Vilenkin N. Ya., Shibasov L. P., Shibasova Z. F. Iza stranica udžbenika matematike. Moskva: Obrazovanje, 1996.

3. Galitsky M.L., Moshkovich M.M., Shvartsburd S.I. Detaljno proučavanje kursa algebre i matematičke analize: smjernice, didaktički materijali.

4.Ivlev B.M., Abramov A.M., Dudnicin Yu.P., Shvartsburd S.I. M.: Obrazovanje, 1990.

5. Petrakov I. S. Matematički krugovi u 8-10 razredima: knj. za nastavnika M.: Obrazovanje, 1987.

6. Sharygin I. F. Izborni predmet matematike. Rješavanje problema tutorial za 10. razred srednje škole - M.: Prosveta, 1989.