Naći jednadžbu tangentne ravni na površinu. Ravan tangenta na površinu. Površina u diferencijalnoj geometriji

02.08.2020Naslov: Gospodarske zgrade

Preuzmite sa Depositfiles

4. TEORIJA POVRŠINA.

4.1 JEDNAČINE POVRŠINE.

Površina u trodimenzionalnom prostoru može se specificirati:

1) implicitno: F ( x , y , z ) =0 (4.1)

2) eksplicitno: z = f ( x , y ) (4.2)

3) parametarski: (4.3)

ili:
(4.3’)

gdje su skalarni argumenti
ponekad se nazivaju krivolinijskim koordinatama. Na primjer, sfera
zgodno je odrediti u sfernim koordinatama:
.

4.2 TANGENTNA RAVNINA I NORMALNA NA POVRŠINU.

Ako pravac leži na površini (4.1), tada koordinate njenih tačaka zadovoljavaju jednadžbu površine:

Razlikovanjem ovog identiteta dobijamo:

(4.4)

ili
(4.4 ’ )

u svakoj tački na krivulji na površini. Dakle, vektor gradijenta u nesingularnim tačkama površine (u kojoj je funkcija (4.5) diferencibilna i
) je okomita na vektore tangente na bilo koje prave na površini, tj. može se koristiti kao normalni vektor za sastavljanje jednadžbe tangentne ravnine u tački M 0 (x 0 , y 0 , z 0 ) površina

(4.6)

i kao vektor smjera u normalnoj jednadžbi:

(4.7)

U slučaju eksplicitne (4.2) specifikacije površine, jednačine tangentne ravni i normale, respektivno, imaju oblik:

(4.8)

I
(4.9)

Sa parametarskim prikazom površine (4.3), vektori
leže u tangentnoj ravni i jednačina tangentne ravni se može napisati kao:

(4.10)

a njihov vektorski proizvod se može uzeti kao vektor normale smjera:

a normalna jednačina se može napisati kao:

(4.11)

Gdje
— vrijednosti parametara koje odgovaraju tački M 0 .

U nastavku ćemo se ograničiti na razmatranje samo onih tačaka površine gdje su vektori

nije jednako nuli i nije paralelno.

Primjer 4.1 Napravite jednadžbe za tangentnu ravan i normalu u tački M 0 (1,1,2) na površinu paraboloida okretanja
.

Rješenje: Pošto je paraboloidna jednadžba data eksplicitno, onda prema (4.8) i (4.9) moramo pronaći
u tački M 0 :

, a u tački M 0
. Tada jednačina tangentne ravni u tački M 0 će izgledati ovako:

2(x -1)+2(y -1)-(z-2)=0 ili 2 x +2 y – z - 2=0, i normalna jednačina
.

Primjer 4.2 Sastavite jednadžbe za tangentnu ravan i normalu u proizvoljnoj tački helikoida
, .

Rješenje. ovdje,

Jednadžba tangentne ravni:

ili

Normalne jednačine:

4.3 PRVI KVADRATNI POVRŠINSKI OBLIK.

Ako je površina data jednadžbom

zatim kriva
može se dati jednačinom
(4.12)

Diferencijal radijus vektora
duž krive, što odgovara pomaku od tačke M 0 do najbliže tačke M, jednako je

(4.13)

Jer
je diferencijal luka krive koji odgovara istom pomaku), tada

(4.14)

Gdje .

Izraz na desnoj strani (4.14) naziva se prvim kvadratnim oblikom površine i igra veliku ulogu u teoriji površina.

Integrišem diferencijalds u rasponu od t 0 (odgovara tački M 0 ) do t (odgovara tački M), dobijamo dužinu odgovarajućeg segmenta krive

(4.15)

Poznavajući prvi kvadratni oblik površine, možete pronaći ne samo dužine, već i uglove između krivih.

Ako du , dv su diferencijali krivolinijskih koordinata koje odgovaraju beskonačno malom pomaku duž jedne krive, i
- s druge strane, tada uzimajući u obzir (4.13):

(4.16)

Korištenje formule

(4.17)

prvi kvadratni oblik omogućava izračunavanje površine regije
površine.

Primjer 4.3 Na helikoidu pronađite dužinu heliksa
između dve tačke.

Rješenje. Jer na spirali
, To . Hajde da nađemo tačku
prvi kvadratni oblik. Odredivši iv = t , dobijamo jednačinu ove spiralne linije u obliku . kvadratni oblik:

= - prvi kvadratni oblik.

Evo. U formuli (4.15) u ovom slučaju
i dužina luka:

4.4 DRUGI KVADRATNI POVRŠINSKI OBLIK.

Označimo
- jedinični vektor normalan na površinu
:

(4.18) . (4.23)

Prava na površini naziva se linija zakrivljenosti ako je njen smjer u svakoj tački glavni smjer.

4.6 POJAM GEODETSKIH LINIJA NA POVRŠINI.

Definicija 4.1 . Krivulja na površini naziva se geodetska ako je njena glavna normala u svakoj tački u kojoj je zakrivljenost različita od nule, ona se poklapa sa normalom na površinu.

Kroz svaku tačku površine u bilo kojem smjeru prolazi, i to samo jedna geodetska. Na sferi, na primjer, veliki krugovi su geodetske.

Parametarizacija površine naziva se polugeodetskom ako se jedna porodica koordinatnih linija sastoji od geodezija, a druga je ortogonalna na nju. Na primjer, na sferi postoje meridijani (geodezije) i paralele.

Geodezija na dovoljno malom segmentu je najkraća od svih krivih koje su joj blizu koje spajaju iste tačke.

Naime, o onome što vidite u naslovu. U suštini, ovo je "prostorni analog" problemi nalaženja tangente I normalni na graf funkcije jedne varijable, te stoga ne bi trebalo nastati poteškoće.

Počnimo s osnovnim pitanjima: ŠTA JE tangentna ravan i ŠTA JE normala? Mnogi ljudi razumiju ove koncepte na nivou intuicije. Najjednostavniji model koji vam pada na pamet je lopta na kojoj leži tanak ravan komad kartona. Karton se nalazi što bliže sferi i dodiruje je u jednoj tački. Osim toga, na mjestu kontakta osiguran je iglom koja zabode ravno prema gore.

U teoriji, postoji prilično genijalna definicija tangentne ravni. Zamislite besplatno površine i tačka koja joj pripada. Očigledno, mnogo toga prolazi kroz tačku prostorne linije, koji pripadaju ovoj površini. Ko ima kakve asocijacije? =) ...lično sam zamislio hobotnicu. Pretpostavimo da svaka takva linija ima prostorna tangenta u tački .

Definicija 1: tangentna ravan na površinu u jednoj tački - ovo je avion, koji sadrži tangente na sve krive koje pripadaju datoj površini i prolaze kroz tačku.

Definicija 2: normalno na površinu u jednoj tački - ovo je ravno, prolazeći kroz datu tačku okomito na tangentnu ravan.

Jednostavno i elegantno. Usput, kako ne biste umrli od dosade od jednostavnosti materijala, malo kasnije podijelit ću s vama jednu elegantnu tajnu koja vam omogućava da zaboravite na trpanje raznih definicija JEDNOM ZA SVAKADA.

Upoznajmo se s radnim formulama i algoritmom rješenja na konkretnom primjeru. U velikoj većini problema potrebno je konstruirati i jednadžbu tangentne ravni i normalnu jednačinu:

Primjer 1

Rješenje:ako je površina data jednadžbom (tj. implicitno), tada se jednadžba tangentne ravnine na datu površinu u tački može naći pomoću sljedeće formule:

Posebnu pažnju obraćam na neobične parcijalne derivate - njihove ne treba zbuniti With parcijalni derivati implicitno specificirane funkcije (iako je površina specificirana implicitno). Prilikom pronalaženja ovih derivata mora se voditi pravila za diferenciranje funkcije od tri varijable, to jest, kada se diferencira u odnosu na bilo koju varijablu, druga dva slova se smatraju konstantama:

Bez napuštanja kase nalazimo parcijalni derivat u tački:

Isto tako:

Ovo je bio najneugodniji trenutak odluke, u kojem se greška, ako nije dozvoljena, onda stalno pojavljuje. Međutim, ovdje postoji efikasna tehnika verifikacije, o kojoj sam govorio na času. Usmjerena derivacija i gradijent.

Svi "sastojci" su pronađeni i sada je stvar pažljive zamjene uz daljnja pojednostavljenja:

– opšta jednačinaželjenu tangentnu ravan.

Toplo preporučujem da provjerite i ovu fazu rješenja. Prvo morate biti sigurni da koordinate tačke tangente zaista zadovoljavaju pronađenu jednadžbu:

- istinska jednakost.

Sada „skidamo“ koeficijente opšta jednačina ravnine i provjerite ih na podudarnost ili proporcionalnost sa odgovarajućim vrijednostima. U ovom slučaju oni su proporcionalni. Kao što se sećate iz kurs analitičke geometrije, - Ovo normalni vektor tangentna ravan, a on je takođe vodeći vektor normalna prava linija. Hajde da komponujemo kanonske jednačine normale po tački i vektoru smjera:

U principu, nazivnici se mogu smanjiti za dva, ali za to nema posebne potrebe

Odgovori:

Nije zabranjeno jednadžbe označavati nekim slovima, ali, opet, zašto? Ovde je već krajnje jasno šta je šta.

Sljedeća dva primjera možete sami riješiti. Mala "matematička vrtoglavica jezika":

Primjer 2

Naći jednačine tangentne ravni i normale na površinu u tački.

I zadatak koji je zanimljiv sa tehničke tačke gledišta:

Primjer 3

Napišite jednadžbe za tangentnu ravan i normalu na površinu u tački

U tački.

Sva je prilika da se ne samo zbunite, već i naiđete na poteškoće prilikom snimanja kanonske jednadžbe prave. A normalne jednačine, kao što verovatno razumete, obično se pišu u ovom obliku. Iako je, zbog zaborava ili nepoznavanja nekih nijansi, parametarski oblik više nego prihvatljiv.

Približni primjeri konačnog izvođenja rješenja na kraju lekcije.

Postoji li tangentna ravan u bilo kojoj tački površine? Generalno, naravno da ne. Klasičan primjer je konusna površina i tačka - tangente u ovoj tački direktno formiraju konusnu površinu i, naravno, ne leže u istoj ravni. Lako je analitički provjeriti da nešto nije u redu: .

Drugi izvor problema je činjenica nepostojanje bilo koji parcijalni izvod u tački. Međutim, to ne znači da u datoj tački ne postoji jedna tangentna ravan.

Ali to je prije bila popularna naučna nego praktično značajna informacija, i vraćamo se na hitne stvari:

Kako napisati jednadžbe za tangentnu ravan i normalu u tački,
ako je površina specificirana eksplicitnom funkcijom?

Prepišimo to implicitno:

I koristeći iste principe nalazimo parcijalne derivate:

Tako se formula tangentne ravni pretvara u sljedeću jednačinu:

I prema tome, kanonske normalne jednadžbe:

Kao što možete pretpostaviti, - ovo su već "stvarni" parcijalni derivati funkcije dvije varijable na tački koju smo označavali slovom “z” i pronađeni su 100500 puta.

Imajte na umu da je u ovom članku dovoljno zapamtiti prvu formulu, iz koje je, ako je potrebno, lako izvesti sve ostalo (naravno, sa osnovnim nivoom obuke). Upravo to je pristup koji treba koristiti prilikom proučavanja egzaktnih nauka, tj. iz minimuma informacija moramo težiti da „izvučemo“ maksimum zaključaka i posledica. „Razmatranje“ i postojeće znanje će pomoći! Ovaj princip je također koristan jer će vas najvjerovatnije spasiti u kritičnoj situaciji kada znate vrlo malo.

Razradimo "modificirane" formule s nekoliko primjera:

Primjer 4

Napišite jednadžbe za tangentnu ravan i normalu na površinu u tački .

Ovdje je malo preklapanje sa notacijama - sada slovo označava tačku na ravni, ali šta da se radi - tako popularno slovo...

Rješenje: sastavimo jednačinu željene tangentne ravni koristeći formulu:

Izračunajmo vrijednost funkcije u tački:

Hajde da izračunamo Parcijalni derivati 1. reda u ovom trenutku:

ovako:

pažljivo, ne žuri:

Zapišimo kanonske jednadžbe normale u tački:

Odgovori:

I konačni primjer za vaše vlastito rješenje:

Primjer 5

Zapišite jednadžbe za tangentnu ravan i normalu na površinu u tački.

Konačno - jer sam objasnio bukvalno sve tehničke tačke i nemam šta posebno dodati. Čak su i same funkcije predložene u ovom zadatku dosadne i monotone - u praksi je gotovo sigurno da ćete naići na "polinom", a u tom smislu primjer br. 2 s eksponentom izgleda kao "crna ovca". Inače, mnogo je vjerojatnije da ćete naići na površinu definiranu jednadžbom, a to je još jedan razlog zašto je funkcija uključena u članak kao broj dva.

I na kraju, obećana tajna: pa kako izbjeći trpanje definicija? (Ne mislim, naravno, na situaciju kada student grozničavo trpa nešto prije ispita)

Definicija svakog pojma/pojave/predmeta, prije svega, daje odgovor na sljedeće pitanje: ŠTA JE TO? (ko/takvi/takvi/su). Svesno Kada odgovarate na ovo pitanje, trebali biste pokušati razmisliti značajan znakovi, definitivno identificiranje određenog pojma/fenomena/objekta. Da, isprva se ispostavi da je pomalo na jeziku, neprecizan i suvišan (nastavnik će vas ispraviti =)), ali s vremenom se razvija sasvim pristojan naučni govor.

Vježbajte na najapstraktnijim objektima, na primjer, odgovorite na pitanje: ko je Čeburaška? Nije baš tako jednostavno ;-) Da li je ovo “lik iz bajke sa velikim ušima, očima i smeđim krznom”? Daleko i veoma daleko od definicije - nikad se ne zna da postoje likovi sa takvim karakteristikama... Ali ovo je mnogo bliže definiciji: „Čeburaška je lik koji je izmislio pisac Eduard Uspenski 1966. godine, koji je ... (popis glavnih karakteristične karakteristike)» . Obratite pažnju kako je dobro počelo

Neka nam je površina definisana jednadžbom oblika

Hajde da uvedemo sljedeću definiciju.

Definicija 1. Prava linija se naziva tangenta na površinu u nekoj tački ako jeste

tangenta na bilo koju krivulju koja leži na površini i prolazi kroz tačku.

Budući da beskonačan broj različitih krivulja koje leže na površini prolazi kroz tačku P, onda će, općenito govoreći, postojati beskonačan broj tangenti na površinu koja prolazi kroz ovu tačku.

Hajde da uvedemo pojam singularnih i običnih tačaka površine

Ako su u nekoj tački sva tri izvoda jednaka nuli ili barem jedan od ovih izvoda ne postoji, tada se tačka M naziva singularna tačka površine. Ako u nekoj tački postoje sve tri derivacije i kontinuirane su, a barem jedan od njih je različit od nule, tada se tačka M naziva običnom tačkom površine.

Sada možemo formulirati sljedeću teoremu.

Teorema. Sve tangente na datu površinu (1) u njenoj običnoj tački P leže u istoj ravni.

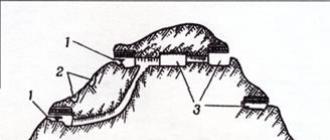
Dokaz. Razmotrimo određenu pravu L na površini (slika 206) koja prolazi kroz datu tačku P površine. Neka je kriva koja se razmatra data parametarskim jednadžbama

Tangenta na krivu će biti tangenta na površinu. Jednačine ove tangente imaju oblik

Ako se izrazi (2) zamijene u jednačinu (1), onda će se ova jednačina pretvoriti u identičnost u odnosu na t, jer kriva (2) leži na površini (1). Razlikujući ga po dobijamo

Projekcije ovog vektora zavise od - koordinata tačke P; imajte na umu da pošto je tačka P obična, ove projekcije u tački P ne nestaju istovremeno i stoga

tangenta na krivulju koja prolazi kroz tačku P i leži na površini. Projekcije ovog vektora su izračunate na osnovu jednačina (2) na vrijednosti parametra t koji odgovara tački P.

Izračunajmo skalarni proizvod vektora N i koji je jednak zbroju proizvoda istoimenih projekcija:

Na osnovu jednakosti (3), izraz na desnoj strani jednak je nuli, dakle,

Iz posljednje jednakosti slijedi da su vektor LG i vektor tangente na krivu (2) u tački P okomiti. Gornje razmišljanje vrijedi za bilo koju krivulju (2) koja prolazi kroz tačku P i leži na površini. Prema tome, svaka tangenta na površinu u tački P je okomita na isti vektor N i stoga sve ove tangente leže u istoj ravni okomito na vektor LG. Teorema je dokazana.

Definicija 2. Ravan u kojoj se nalaze sve tangente na prave na površini koje prolaze kroz njenu datu tačku P naziva se tangentna ravan na površinu u tački P (Sl. 207).

Imajte na umu da u pojedinačnim tačkama površine možda ne postoji tangentna ravan. U takvim tačkama, tangente na površinu možda neće ležati u istoj ravni. Na primjer, vrh konične površine je singularna tačka.

Tangente na konusnu površinu u ovoj tački ne leže u istoj ravni (one same tvore konusnu površinu).

Zapišimo jednačinu tangentne ravni na površinu (1) u običnoj tački. Kako je ova ravan okomita na vektor (4), njena jednadžba ima oblik

Ako je jednadžba površine data u obliku ili jednačina tangentne ravni u ovom slučaju ima oblik

Komentar. Ako unesemo formulu (6), onda će ova formula dobiti oblik

njegova desna strana je potpuni diferencijal funkcije. Dakle, . Dakle, ukupni diferencijal funkcije dvije varijable u tački koja odgovara prirastu nezavisnih varijabli x i y jednak je odgovarajućem inkrementu primjene tangentne ravni na površinu, što je graf ove funkcije.

Definicija 3. Prava linija povučena kroz tačku na površini (1) okomitu na tangentnu ravan naziva se normala na površinu (Sl. 207).

Napišimo normalne jednačine. Budući da se njegov smjer poklapa sa smjerom vektora N, njegove jednačine će imati oblik

Površina je definirana kao skup tačaka čije koordinate zadovoljavaju određeni tip jednačine:

F (x, y, z) = 0 (1) (\displaystyle F(x,\,y,\,z)=0\qquad (1))

Ako je funkcija F (x, y, z) (\displaystyle F(x,\,y,\,z)) je kontinuirana u nekoj tački i ima kontinuirane parcijalne derivacije u sebi, od kojih barem jedan ne nestaje, tada će u okolini ove tačke površina data jednadžbom (1) biti desnu površinu.

Pored navedenog implicitni način specificiranja, površina se može definirati očigledno, ako se jedna od varijabli, na primjer, z, može izraziti u terminima ostalih:

z = f (x, y) (1 ′) (\displaystyle z=f(x,y)\qquad (1"))

Još strožije jednostavna površina se naziva slikom homeomorfnog preslikavanja (to jest, jedan-na-jedan i međusobno kontinuirano preslikavanje) unutrašnjosti jediničnog kvadrata. Ovoj definiciji se može dati analitički izraz.

Pustite u avion sa pravougaoni sistem koordinate u i v, dat je kvadrat čije koordinate unutrašnjih tačaka zadovoljavaju nejednakosti 0< u < 1, 0 < v < 1. Гомеоморфный образ квадрата в пространстве с прямоугольной системой координат х, у, z задаётся при помощи формул х = x(u, v), у = y(u, v), z = z(u, v) (параметрическое задание поверхности). При этом от функций x(u, v), y(u, v) и z(u, v) требуется, чтобы они были непрерывными и чтобы для различных точек (u, v) и (u", v") были различными соответствующие точки (x, у, z) и (x", у", z").

Primjer jednostavna površina je hemisfera. Cijela sfera nije jednostavna površina. Ovo iziskuje dalju generalizaciju koncepta površine.

Podskup prostora, čija svaka tačka ima susjedstvo koje je jednostavna površina, zvao desnu površinu .

Površina u diferencijalnoj geometriji

Helicoid

Katenoid

metrika ne određuje jednoznačno oblik površine. Na primjer, metrike helikoida i katenoida, parametrizirane u skladu s tim, poklapaju se, odnosno postoji korespondencija između njihovih regija koja čuva sve dužine (izometrija). Svojstva koja se čuvaju pod izometrijskim transformacijama nazivaju se unutrašnja geometrija površine. Unutrašnja geometrija ne zavisi od položaja površine u prostoru i ne menja se kada je savijena bez napetosti ili kompresije (na primer, kada je cilindar savijen u konus).

Metrički koeficijenti E , F , G (\displaystyle E,\ F,\ G) određuju ne samo dužine svih krivih, već i općenito rezultate svih mjerenja unutar površine (uglovi, površine, zakrivljenost, itd.). Dakle, sve što zavisi samo od metrike odnosi se na unutrašnju geometriju.

Normalni i normalni dio

Normalni vektori u tačkama površine

Jedna od glavnih karakteristika površine je njena normalno- jedinični vektor okomit na tangentnu ravan u datoj tački:

m = [ r u ′ , r v ′ ] |.

[ r u ′ , r v ′ ] |

(\displaystyle \mathbf (m) =(\frac ([\mathbf (r"_(u)) ,\mathbf (r"_(v)) ])(|[\mathbf (r"_(u)) ,\mathbf (r"_(v)) ]|))) Predznak normale zavisi od izbora koordinata. Presjek površine ravninom koja sadrži površinu normalnu u datoj tački formira određenu krivu koja se naziva

normalna sekcija površine. Glavna normala za normalni presjek poklapa se s normalom na površinu (do predznaka). Ako kriva na površini nije normalan presjek, tada njena glavna normala tvori određeni kut s normalom površine θ (\displaystyle \theta) krivulja povezana sa zakrivljenošću k n (\displaystyle k_(n)) normalni presjek (sa istom tangentom) po Meunierovoj formuli:

k n = ± k cos θ (\displaystyle k_(n)=\pm k\,\cos \,\theta )

Koordinate normalnog jediničnog vektora za različite načine zadaci površina su dati u tabeli:

	Normalne koordinate u tački površine
implicitno zadavanje	(∂ F ∂ x ; ∂ F ∂ y ; ∂ F ∂ z) (∂ F ∂ x) 2 + (∂ F ∂ y) 2 + (∂ F ∂ z) 2 (\displaystyle (\frac (\left(( \frac (\partial F)(\partial x));\,(\frac (\partial F)(\partial y));\,(\frac (\partial F)(\partial z))\right) )(\sqrt (\left((\frac (\partial F)(\partial x))\right)^(2)+\left((\frac (\partial F)(\partial y))\right) ^(2)+\lijevo((\frac (\djelomično F)(\djelomično z))\desno)^(2)))))
eksplicitni zadatak	(− ∂ f ∂ x ; − ∂ f ∂ y ; 1) (∂ f ∂ x) 2 + (∂ f ∂ y) 2 + 1 (\displaystyle (\frac (\left(-(\frac (\partial f) )(\partial x));\,-(\frac (\partial f)(\partial y));\,1\right))(\sqrt (\left((\frac (\partial f)(\ djelomično x))\desno)^(2)+\lijevo((\frac (\djelomično f)(\djelomično y))\desno)^(2)+1))))
parametarska specifikacija	(D (y, z) D (u, v) ; D (z, x) D (u, v) ; D (x, y) D (u, v)) (D (y, z) D (u , v)) 2 + (D (z, x) D (u, v)) 2 + (D (x, y) D (u, v)) 2 (\displaystyle (\frac (\left((\frac (D(y,z))(D(u,v)));\,(\frac (D(z,x))(D(u,v)));\,(\frac (D(x) ,y))(D(u,v)))\desno))(\sqrt (\levo((\frac (D(y,z))(D(u,v)))\desno)^(2 )+\left((\frac (D(z,x))(D(u,v)))\desno)^(2)+\left((\frac (D(x,y))(D( u,v)))\desno)^(2))))

Evo D (y, z) D (u, v) = |.

y u ′ y v ′ z u ′ z v ′ | , D (z, x) D (u, v) = |.

z u ′ z v ′ x u ′ x v ′ |

, D (x, y) D (u, v) = | x u ′ x v ′ y u ′ y v ′ |(\displaystyle (\frac (D(y,z))(D(u,v)))=(\begin(vmatrix)y"_(u)&y"_(v)\\z"_(u) &z"_(v)\end(vmatrix)),\quad (\frac (D(z,x))(D(u,v)))=(\begin(vmatrix)z"_(u)&z" _(v)\\x"_(u)&x"_(v)\end(vmatrix)),\quad (\frac (D(x,y))(D(u,v)))=(\ begin(vmatrix)x"_(u)&x"_(v)\\y"_(u)&y"_(v)\end(vmatrix))) Svi derivati se uzimaju u tački(x 0 , y 0 , z 0) (\displaystyle (x_(0),y_(0),z_(0)))

Uopšteno govoreći, u svakoj tački na površini postoje dva okomita pravca e 1 (\displaystyle e_(1)) I e 2 (\displaystyle e_(2)), u kojem normalna krivina poprima minimalne i maksimalne vrijednosti; ovi pravci se nazivaju main. Izuzetak je slučaj kada je normalna zakrivljenost u svim smjerovima ista (na primjer, blizu sfere ili na kraju elipsoida okretanja), tada su svi pravci u tački glavni.

Površine sa negativnom (lijevo), nultom (u sredini) i pozitivnom (desno) zakrivljenjem.

Normalne zakrivljenosti u glavnim pravcima nazivaju se glavne krivine; označimo ih κ 1 (\displaystyle \kappa _(1)) I κ 2 (\displaystyle \kapa _(2)). Veličina:

K = κ 1 κ 2 (\displaystyle K=\kappa _(1)\kappa _(2))

Graf funkcije 2 varijable z = f(x,y) je površina projektovana na ravan XOY u domenu definicije funkcije D.
Razmotrite površinu σ , dat jednadžbom z = f(x,y), gdje je f(x,y) diferencijabilna funkcija, a neka je M 0 (x 0 ,y 0 ,z 0) fiksna tačka na površini σ, tj. z 0 = f(x 0 ,y 0). Svrha. Online kalkulator je dizajniran za pronalaženje tangentne ravni i normalne jednačine površine. Rješenje je sastavljeno u Word formatu. Ako trebate pronaći jednadžbu tangente na krivu (y = f(x)), onda trebate koristiti ovu uslugu.

Pravila za unos funkcija:

Sve varijable su izražene kroz x,y,z

Tangentna ravan na površinu σ na njenom mestu M 0 je ravan u kojoj leže tangente na sve krive nacrtane na površini σ kroz tačku M 0 .
Jednačina tangentne ravni na površinu definisanu jednadžbom z = f(x,y) u tački M 0 (x 0 ,y 0 ,z 0) ima oblik:

z – z 0 = f’ x (x 0 ,y 0)(x – x 0) + f’ y (x 0 ,y 0)(y – y 0)

Vektor se naziva vektor normalne površine σ u tački M 0. Vektor normale je okomit na tangentnu ravan.
Normalno na površinu σ u tački M 0 je prava koja prolazi kroz ovu tačku i ima smjer vektora N.
Kanonske jednadžbe normale na površinu definirane jednadžbom z = f(x,y) u tački M 0 (x 0 ,y 0 ,z 0), gdje je z 0 = f(x 0 ,y 0), imaju oblik:

Primjer br. 1. Površina je data jednadžbom x 3 +5y. Naći jednačinu tangentne ravni na površinu u tački M 0 (0;1).
Rješenje. Zapišimo tangentne jednačine opšti pogled: z - z 0 = f" x (x 0 ,y 0 ,z 0)(x - x 0) + f" y (x 0 ,y 0 ,z 0)(y - y 0)
Prema uslovima zadatka, x 0 = 0, y 0 = 1, zatim z 0 = 5
Nađimo parcijalne izvode funkcije z = x^3+5*y:
f" x (x,y) = (x 3 +5 y)" x = 3 x 2
f" x (x,y) = (x 3 +5 y)" y = 5
U tački M 0 (0,1) vrijednosti parcijalnih izvoda su:
f" x (0;1) = 0
f" y (0;1) = 5
Koristeći formulu, dobijamo jednačinu tangentne ravni na površinu u tački M 0: z - 5 = 0(x - 0) + 5(y - 1) ili -5 y+z = 0

Primjer br. 2. Površina je definirana implicitno y 2 -1/2*x 3 -8z. Naći jednadžbu tangentne ravni na površinu u tački M 0 (1;0;1).
Rješenje. Pronalaženje parcijalnih izvoda funkcije. Pošto je funkcija specificirana implicitno, tražimo derivate koristeći formulu:

Za našu funkciju:

onda:

U tački M 0 (1,0,1) vrijednosti parcijalnih izvoda:
f" x (1;0;1) = -3 / 16
f" y (1;0;1) = 0
Koristeći formulu, dobijamo jednačinu tangentne ravni na površinu u tački M 0: z - 1 = -3 / 16 (x - 1) + 0(y - 0) ili 3 / 16 x+z- 19 / 16 = 0

Primjer. Površina σ dato jednačinom z= y/x + xy – 5x 3. Naći jednadžbu tangentne ravni i normale na površinu σ u tački M 0 (x 0 ,y 0 ,z 0), koji joj pripada, ako x 0 = –1, y 0 = 2.
Nađimo parcijalne izvode funkcije z= f(x,y) = y/x + xy – 5x 3:
f x '( x,y) = (y/x + xy – 5x 3)’ x = – y/x 2 + y – 15x 2 ;
f y ' ( x,y) = (y/x + xy – 5x 3)’ y = 1/x + x.
Dot M 0 (x 0 ,y 0 ,z 0) pripada površini σ , pa možemo izračunati z 0 , zamjenjujući dato x 0 = –1 i y 0 = 2 u jednadžbu površine:

z= y/x + xy – 5x 3

z 0 = 2/(-1) + (–1) 2 – 5 (–1) 3 = 1.
U tački M 0 (–1, 2, 1) parcijalne derivacijske vrijednosti:
f x '( M 0) = –1/(-1) 2 + 2 – 15(–1) 2 = –15; f y '( M 0) = 1/(-1) – 1 = –2.
Koristeći formulu (5) dobijamo jednačinu tangentne ravni na površinu σ u tački M 0:
z – 1= –15(x + 1) – 2(y – 2) z – 1= –15x – 15 – 2y + 4 15x + 2y + z + 10 = 0.
Koristeći formulu (6) dobijamo kanonske jednadžbe normale na površinu σ u tački M 0:

.
Odgovori: jednačina tangentne ravni: 15 x + 2y + z+ 10 = 0; normalne jednadžbe:

Primjer br. 1. Date su funkcije z=f(x,y) i dvije točke A(x 0, y 0) i B(x 1, y 1). Potrebno: 1) izračunati vrijednost z 1 funkcije u tački B; 2) izračunati približnu vrednost z 1 funkcije u tački B na osnovu vrednosti z 0 funkcije u tački A, zamenjujući prirast funkcije pri kretanju od tačke A do tačke B sa diferencijalom; 3) kreirati jednačinu za tangentnu ravan na površinu z = f(x,y) u tački C(x 0 ,y 0 ,z 0).
Rješenje.
Zapišimo tangentne jednačine u opštem obliku:
z - z 0 = f" x (x 0 ,y 0 ,z 0)(x - x 0) + f" y (x 0 ,y 0 ,z 0)(y - y 0)
Prema uslovima zadatka, x 0 = 1, y 0 = 2, zatim z 0 = 25
Nađimo parcijalne izvode funkcije z = f(x,y)x^2+3*x*y*+y^2:
f" x (x,y) = (x 2 +3 x y +y 2)" x = 2 x+3 y 3
f" x (x,y) = (x 2 +3 x y +y 2)" y = 9 x y 2
U tački M 0 (1,2) vrijednosti parcijalnih izvoda su:
f" x (1;2) = 26
f" y (1;2) = 36
Koristeći formulu, dobijamo jednačinu tangentne ravni na površinu u tački M 0:
z - 25 = 26(x - 1) + 36(y - 2)
ili
-26 x-36 y+z+73 = 0

Primjer br. 2. Napišite jednadžbe tangentne ravni i normale na eliptični paraboloid z = 2x 2 + y 2 u tački (1;-1;3).